
【题目】(1)如图,线段AB上有两个点C、D,请计算图中共有多少条线段?
![]()
(2)如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?
(3)拓展应用:8个班级参加学校组织的篮球比赛,比赛采用单循环制(即每两个班级之间都要进行一场比赛),那么一共要进行多少场比赛?
【答案】(1)6条;(2)![]() ;(3)
;(3)![]() .
.
【解析】
对于(1),从左向右依次固定一个端点A、C、D找出线段,再求和即可;
对于(2),根据数线段的特点列出式子并化简,就能解答本问;
对于(3),将实际问题转化成(2)的模型,借助(2)的结论解答.
(1)∵以点A为左端点向右的线段有:线段AB、AC、AD,
以点C为左端点向右的线段有线段CD、CB,
以点D为左端点的线段有线段DB,
∴共有3+2+1=6条线段;
(2)![]() .理由如下:
.理由如下:
设线段上有m个点,该线段上共有线段x条,
则x=(m-1)+(m-2)+(m-3)+…+3+2+1,
∴倒序排列有x=1+2+3+…+(m-3)+(m-2)+(m-1),
∴2x=m(m-1),
![]() ,
,
故有![]() 条线段;
条线段;
(3)把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作为一条线段,
直线上8个点所构成的线段条数就等于比赛的场数,
因此一共要进行![]() 场比赛.
场比赛.


科目:初中数学 来源: 题型:
【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )

A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
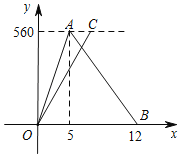
【题目】一天,明明和强强相约到距他们村庄560米的博物馆游玩,他们同时从村庄出发去博物馆,明明到博物馆后因家中有事立即返回.如图是他们离村庄的距离y(米)与步行时间x(分钟)之间的函数图象,若他们出发后6分钟相遇,则相遇时强强的速度是_____米/分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=3
,AH=3![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
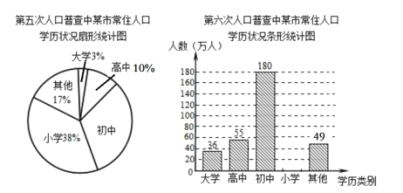
【题目】根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如图所示(部分信息未给出):
解答下列问题:
(1)求第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)求第五次人口普查中该市常住人口每万人中具有初中学历的人数;
(3)第六次人口普查结果与第五次相比,每万人中初中学历的人数增加了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图;B类杨梅深加工后再销售,深加工总费用s(万元)与加工数量t(吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入﹣经营总成本)
(3)若该公司收购20吨杨梅,要使该公司获得30万元毛利润,求直销的A类杨梅有多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a,宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为_________;小正方形(阴影部分)的边长为_________.(用含a,b的代数式表示)
(2)仔细观察图,请你写出下列三个代数式(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系.
(3)已知a+b=7,ab=6,求代数式(a-b)2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com