
| A. | 36n mile | B. | 48n mile | C. | 60n mile | D. | 54n mile |
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
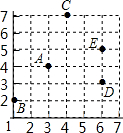 张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )
张萌在纸上画了一个如图所示的网格图,每个小格的边长都是1个单位长度,点A,B,C,D,E都在格点上,若张萌将点E表示成(6,5),则下列四点表示不正确的是( )| A. | 点A表示成(3,4) | B. | 点B表示成(2,1) | C. | 点C表示成(4,7) | D. | 点D表示成(6,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
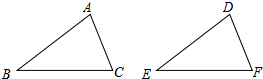 如图,给出下列四组条件:
如图,给出下列四组条件:| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
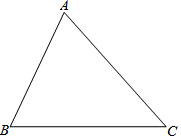 如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.
如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com