Question

5．如图，抛物线y=ax²+$\frac{7}{2}$x+c（a≠0）与x轴交于点A、B，与直线y=kx+2交于点D、B，点D在y轴上，已知tan∠DBO=$\frac{1}{2}$．作垂直x轴的直线x=t，与线段DB交于点E，与抛物线交于点F．
（1）求抛物线解析式和直线DB解析式；
（2）连接OE、DF，当S_{四边形DOEF}=$\frac{3}{2}$S_△EFD时，求线段OE的长；
（3）点Q是平面内一点，以点D、E、F、Q为顶点作菱形，求点E的坐标．

Answer 1

分析 （1）根据直线y=kx+2与y轴交于点D，求出点D的坐标，根据tan∠DBO=$\frac{1}{2}$，求出点B的坐标，再根据$\left\{\begin{array}{l}{2=c}\\{0=16a+\frac{7}{2}×4+c}\end{array}\right.$，求出抛物线解析式，根据直线y=kx+2过点B，得出0=4k+2，求出k即可；
（2）设EF与x轴交与点M，先求出EF=-t²+4t，得出S_{四边形DOEF}=$\frac{1}{2}$×[2+（-t²+4t）]×t，S_△EFD=$\frac{1}{2}$×（-t²+4t）×t，再根据S_{四边形DOEF}=$\frac{3}{2}$S_△EFD，
求出t，最后求出EM，即可得出OE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$；
（3）根据点E、F的坐标得出EN=-$\frac{1}{2}$t+2，FN=-t²+$\frac{7}{2}$t+2），
①当DE=DF时，连结DQ，交EF于点M，若D、E、F、Q为顶点作菱形则EM=FM，再根据EM=$\frac{1}{2}$t，FM=-t²+$\frac{7}{2}$t得出$\frac{1}{2}$t=-t²+$\frac{7}{2}$t，求出t后，再求出EN即可得出点E的坐标；
②当DE=DF时，连结DQ，交EF于点M，若D、E、F、Q为顶点作菱形，求出DB=2$\sqrt{5}$，根据$\frac{BE}{BD}$=$\frac{BN}{BO}$，求出BE、DE，从而求出EF，再根据-t²+4t=$\frac{\sqrt{5}}{2}$t求出t，得出EN，即可求出点E的坐标；
③当DF=EF时，过D作DG⊥EF于G，若D、E、F、Q为顶点作菱形，则DG=t，FG=-t²+$\frac{7}{2}$t，根据DF²=t⁴-7t³+$\frac{53}{4}$t²，EF²=16t²-8t³+t⁴得出t⁴-7t³+$\frac{53}{4}$t²=16t²-8t³+t⁴，求出t，得出EN即可求出点E的坐标．

解答 解：（1）∵直线y=kx+2与y轴交于点D，
∴点D的坐标是（0，2），
∵tan∠DBO=$\frac{1}{2}$，
∴$\frac{DO}{BO}$=$\frac{1}{2}$，
∴BO=4，
∴点B的坐标是（4，0），
∴$\left\{\begin{array}{l}{2=c}\\{0=16a+\frac{7}{2}×4+c}\end{array}\right.$，
∴$\left\{\begin{array}{l}{c=2}\\{a=-1}\end{array}\right.$，
∴抛物线解析式是y=-x²+$\frac{7}{2}$x+2
∵直线y=kx+2过点B，
∴0=4k+2
k=-$\frac{1}{2}$，
∴直线DB解析式是y=-$\frac{1}{2}$x+2；

（2）如图1，设EF与x轴交与点M，
∵垂直x轴的直线x=t与线段DB交于点E，与抛物线交于点F，
∴点E、F的坐标是（t，-$\frac{1}{2}$t+2），（t，-t²+$\frac{7}{2}$t+2），
∴EF=（-t²+$\frac{7}{2}$t+2）-（-$\frac{1}{2}$t+2）=-t²+4t，
∴S_{四边形DOEF}=$\frac{1}{2}$×[2+（-t²+4t）]×t，
S_△EFD=$\frac{1}{2}$×（-t²+4t）×t，
∵S_{四边形DOEF}=$\frac{3}{2}$S_△EFD，
∴$\frac{1}{2}$×[2+（-t²+4t）]×t=$\frac{3}{2}$×$\frac{1}{2}$×（-t²+4t）×t，
∴t=2，
∴EM=-$\frac{1}{2}$×2+2=1，
∴OE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$；

（3）∵点E、F的坐标是（t，-$\frac{1}{2}$t+2），（t，-t²+$\frac{7}{2}$t+2），
∴EN=-$\frac{1}{2}$t+2，FN=-t²+$\frac{7}{2}$t+2，
①如图2，当DE=DF时，连结DQ，交EF于点M，若D、E、F、Q为顶点作菱形则EM=FM，
∵EM=2-EN=2-（-$\frac{1}{2}$t+2）=$\frac{1}{2}$t，
FM=FN-2=（-t²+$\frac{7}{2}$t+2）-2=-t²+$\frac{7}{2}$t，
∴$\frac{1}{2}$t=-t²+$\frac{7}{2}$t，
t₁=0（舍去），t₂=3，
∴EN=-$\frac{1}{2}$×3+2=$\frac{1}{2}$，
∴点E的坐标是（3，$\frac{1}{2}$）；
②如图3，当DE=DF时，连结DQ，交EF于点M，若D、E、F、Q为顶点作菱形，
∵OA=2，OB=4，
∴DB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
∵$\frac{BE}{BD}$=$\frac{BN}{BO}$，
∴$\frac{BE}{2\sqrt{5}}$=$\frac{4-t}{4}$，
∴BE=2$\sqrt{5}$-$\frac{\sqrt{5}}{2}$t，
∴DE=2$\sqrt{15}$-（2$\sqrt{5}$-$\frac{\sqrt{5}}{2}$t）=$\frac{\sqrt{5}}{2}$t，
∵EF=（-t²+$\frac{7}{2}$t+2）-（-$\frac{1}{2}$t+2）=-t²+4t，
∴-t²+4t=$\frac{\sqrt{5}}{2}$t，
∴t₁=0，t₂=4-$\frac{\sqrt{5}}{2}$，
∴EN=-$\frac{1}{2}$×（4-$\frac{\sqrt{5}}{2}$）+2=$\frac{\sqrt{5}}{4}$，
∴点E的坐标（4-$\frac{\sqrt{5}}{2}$，$\frac{\sqrt{5}}{4}$）；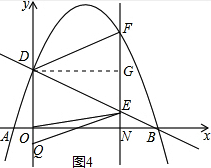
③如图4，当DF=EF时，过D作DG⊥EF于G，若D、E、F、Q为顶点作菱形，
则DG=t，FG=-t²+$\frac{7}{2}$t，
∵DF²=DG²+FG²=t⁴-7t³+$\frac{53}{4}$t²，
EF²=[-（-t²+$\frac{7}{2}$t+2）-（-$\frac{1}{2}$t+2）]²=16t²-8t³+t⁴，
∴t⁴-7t³+$\frac{53}{4}$t²=16t²-8t³+t⁴，
∴t₁=0（舍去），t₂=$\frac{11}{4}$，
∴EN=-$\frac{1}{2}$×$\frac{11}{4}$=2=$\frac{5}{8}$，
∴点E的坐标（$\frac{11}{4}$，$\frac{5}{8}$）．

点评 此题考查了二次函数的综合，用到的知识点是二次函数的图象与性质、菱形的判定与性质、勾股定理等，关键是根据题意画出图形，作出辅助线，注意分类讨论．