
���� ��1��ֱ�����ý���ʽд�������ߵĽ���ʽ��
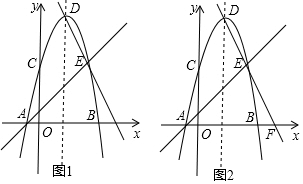
��2����ͼ1�������䷽���õ�D��2��9���������ߵĶԳ���Ϊֱ��x=2����ȷ��C��0��5������E��4��5�����������ô���ϵ�������ֱ��DE�Ľ���ʽΪy=-2x+13��Ȼ�����ȫ�������ε����ʵõ���COQ=��BOQ�����Ե�QΪ��һ����ƽ�����ϵĵ㣬���ⷽ����$\left\{\begin{array}{l}{y=x}\\{y=-2x+13}\end{array}\right.$��Q������ꣻ
��3����ͼ2���Գ��ύx���ڵ�H����ȷ��DH=9��FH=$\frac{9}{2}$��DF=$\frac{9\sqrt{5}}{2}$��AF=$\frac{15}{2}$��AM=2t��FN=$\sqrt{5}$t����FM=$\frac{15}{2}$-2t���������ۣ�����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM����$\sqrt{5}$t=$\frac{15}{2}$-2t������P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q���������ε����ʵ�FQ=$\frac{\sqrt{5}}{2}$t����ͨ���á�FQH�ס�FHD�õ�$\frac{\sqrt{5}}{2}$t��$\frac{9}{2}$=��$\frac{15}{2}$-2t����$\frac{9\sqrt{5}}{2}$������P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3���������ε����ʵ�FK=$\frac{1}{2}$��$\frac{15}{2}$-2t������ͨ����FKN�ס�FHD�õ�$\frac{1}{2}$��$\frac{15}{2}$-2t����$\frac{9}{2}$=$\sqrt{5}$t��$\frac{9\sqrt{5}}{2}$������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬ͨ����FMN�ס�FHD�õ���$\frac{15}{2}$-2t����$\frac{9}{2}$=$\sqrt{5}$t��$\frac{9\sqrt{5}}{2}$������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬ͨ����FNM�ס�FHD�õ���$\frac{15}{2}$-2t����$\frac{9\sqrt{5}}{2}$=$\sqrt{5}$t��$\frac{9}{2}$��Ȼ��ֱ�����t�ķ��̿�ȷ������������t��ֵ��
��� �⣺��1�������ߵĽ���ʽΪy=-��x+1����x-5������y=-x2+4x+5��
��2����ͼ1��y=-x2+4x+5=-��x-2��2+9����D��2��9���������ߵĶԳ���Ϊֱ��x=2��
��x=0ʱ��y=-x2+4x+5=5����C��0��5����
��C��E���������ߵĶԳ���Գƣ�
��E��4��5����
��ֱ��DE�Ľ���ʽΪy=mx+n��
��D��2��9����E��4��5�������$\left\{\begin{array}{l}{2m+n=9}\\{4m+n=5}\end{array}\right.$�����$\left\{\begin{array}{l}{m=-2}\\{n=13}\end{array}\right.$��
��ֱ��DE�Ľ���ʽΪy=-2x+13��
�ߡ�QCO�ա�QBO��
���COQ=��BOQ��
���QΪ��һ����ƽ�����ϵĵ㣬
��OQ�Ľ���ʽΪy=x��
�ⷽ����$\left\{\begin{array}{l}{y=x}\\{y=-2x+13}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{13}{3}}\\{y=\frac{13}{3}}\end{array}\right.$��
��Q���������$\frac{13}{3}$��$\frac{13}{3}$����
��4����ͼ2���Գ��ύx���ڵ�H��DH=9��FH=$\frac{9}{2}$��DF=$\frac{9\sqrt{5}}{2}$��
��y=0ʱ��-2x+13=0�����x=$\frac{13}{2}$����F��$\frac{13}{2}$��0����
��AF=$\frac{13}{2}$-��-1��=$\frac{15}{2}$��
AM=2t��FN=$\sqrt{5}$t����FM=$\frac{15}{2}$-2t��
����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM����$\sqrt{5}$t=$\frac{15}{2}$-2t�����t=$\frac{15\sqrt{5}-30}{2}$��
����P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q����PM��NQ���ഹֱƽ�֣�FQ=$\frac{\sqrt{5}}{2}$t��
�á�FQH�ס�FHD��
��FQ��FH=FM��FD����$\frac{\sqrt{5}}{2}$t��$\frac{9}{2}$=��$\frac{15}{2}$-2t����$\frac{9\sqrt{5}}{2}$�����t=$\frac{5}{3}$��
����P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3����MF��NP���ഹֱƽ�֣�FK=$\frac{1}{2}$MF=$\frac{1}{2}$��$\frac{15}{2}$-2t����
�á�FKN�ס�FHD��
��FK��FH=FN��FD����$\frac{1}{2}$��$\frac{15}{2}$-2t����$\frac{9}{2}$=$\sqrt{5}$t��$\frac{9\sqrt{5}}{2}$�����t=$\frac{15}{8}$��
����P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬
�á�FMN�ס�FHD��
��FM��FH=FN��FD������$\frac{15}{2}$-2t����$\frac{9}{2}$=$\sqrt{5}$t��$\frac{9\sqrt{5}}{2}$�����t=$\frac{5}{2}$��
����P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬
�á�FNM�ס�FHD��
��FM��FD=FN��FH������$\frac{15}{2}$-2t����$\frac{9\sqrt{5}}{2}$=$\sqrt{5}$t��$\frac{9}{2}$�����t=$\frac{15}{14}$��
����������t��ֵΪ$\frac{15\sqrt{5}-30}{2}$��$\frac{5}{3}$��$\frac{15}{8}$��$\frac{5}{2}$��$\frac{15}{14}$��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ��������ʺ�����ƽ���ı��ε��ж������ʣ������ô���ϵ������һ�κ����Ͷ��κ�������ʽ�����������Ʊ��з��̣�����������ͼ�ε����ʣ������÷������۵���ѧ�����ѧ���⣮


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
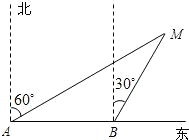 ��ͼ��ij�洬�ϵ�������A����õ���M�ڱ�ƫ��60�㷽�������洬��20����/Сʱ���ٶ������������У���Сʱ����B�㣮��B����õ���M�ڱ�ƫ��30�㷽����B�������M�ľ����Ƕ��ٺ��
��ͼ��ij�洬�ϵ�������A����õ���M�ڱ�ƫ��60�㷽�������洬��20����/Сʱ���ٶ������������У���Сʱ����B�㣮��B����õ���M�ڱ�ƫ��30�㷽����B�������M�ľ����Ƕ��ٺ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
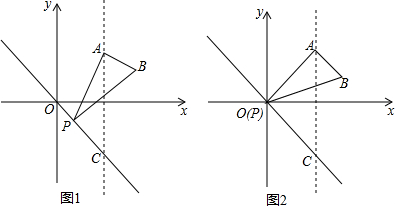
 ��ͼ���ڡ�ABC�У�AB=AC����ACΪֱ������O��BC��D��P��AB�ӳ�����һ�㣬��PC���ҡ�PCB=$\frac{1}{2}$��BAC
��ͼ���ڡ�ABC�У�AB=AC����ACΪֱ������O��BC��D��P��AB�ӳ�����һ�㣬��PC���ҡ�PCB=$\frac{1}{2}$��BAC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
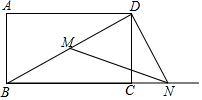 ��֪������ABCD�У�AB=15��AD=20����M�ڶԽ���BD�ϣ���NΪ����BC��һ���㣬����MN��DN���ҡ�DNM=��DBC����DMN�ǵ��������Σ��߶�BN�ij���25��40��$\frac{125}{8}$��
��֪������ABCD�У�AB=15��AD=20����M�ڶԽ���BD�ϣ���NΪ����BC��һ���㣬����MN��DN���ҡ�DNM=��DBC����DMN�ǵ��������Σ��߶�BN�ij���25��40��$\frac{125}{8}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com