Question

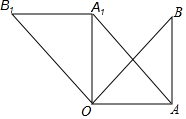
11．如图所示，在Rt△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O沿逆时针方向旋转90°得到△OA₁B₁，连接AA₁．
（1）线段AA₁的长是90°，∠AOB₁的度数是135°；
（2）求证：四边形OAA₁B₁是平行四边形．

Answer 1

分析 （1）直接根据勾股定理即可得出线段AA₁的长，由图形旋转的性质可得出∠AOB₁的度数；
（2）根据图形旋转的性质得出OA=AB=A₁B₁，∠OAB=90°=∠AO A₁=∠O A₁ B₁据此可得出结论．

解答 解：（1）∵△OA₁B₁由△OAB绕点O沿逆时针方向旋转90°得到，
∴OA=OA₁=6，
∴AA₁=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$，∠AOB₁=90°+45°=130°．
故答案为：6$\sqrt{2}$，135°；    
            
（2）∵△OA₁B₁由△OAB绕点O沿逆时针方向旋转90°得到，
∴OA=AB=A₁B₁，∠OAB=90°=∠AO A₁=∠O A₁ B₁，
∴A₁B₁∥AB，
∴四边形OAA₁B₁是平行四边形．

点评 本题考查的是旋转的性质，熟知图形旋转不变性的性质是解答此题的关键．