
已知两个全等的直角三角形纸片ABC、DEF,如图⑴放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.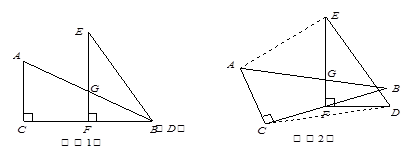
【小题1】求证:△EGB是等腰三角形;
【小题2】若纸片DEF不动,问△ABC绕点F逆时针旋转最小 度时,四边形ACDE成为以ED为底的梯形(如图⑵).求此梯形的高
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
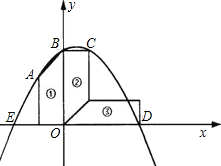 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.查看答案和解析>>
科目:初中数学 来源:2013届四川德阳市中江县柏树中学九年级下学期第一次月考试数学试卷(带解析) 题型:解答题
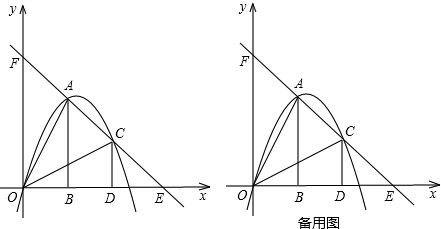
如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.
(1)求该抛物线的函数解析式;
(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2010年浙江省宁波市江东区初三学业水平抽测数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com