
【题目】高空的气温与距地面的高度有关,某地距地面的高度每升高1km,气温下降6℃,已知地面气温为20℃.
(1)写出该地空中气温T(℃)与高度h(km)之间的函数表达式.
(2)求距离地面上4km处的气温T.
(3)求气温为-16℃处距地面的高度h.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
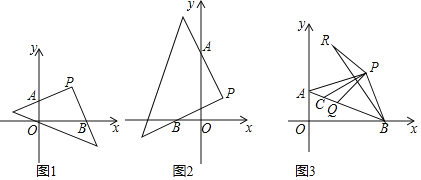
【题目】(1)已知:点P(a,b),P点坐标满足![]() +|3a﹣2b﹣4|=0将45°角的三角板,直角顶点放在P处,两边与坐标轴交于A、B两点,如图1,求a、b的值.
+|3a﹣2b﹣4|=0将45°角的三角板,直角顶点放在P处,两边与坐标轴交于A、B两点,如图1,求a、b的值.
(2)将三角板绕P点,顺时针旋转,两边与x轴交于B点,与y轴交于A点,求|OA﹣OB|的值.
(3)如图3,若Q是线段AB上一动点,C为AQ中点,PR⊥PQ且PR=PQ,连BR,请同学们判断线段BR与PC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学的家与学校的距离均为![]() .甲同学先步行
.甲同学先步行![]() ,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的
,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的![]() 倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到![]() .
.
(1)解:设乙同学骑自行车的速度为![]() .完成表格:
.完成表格:
乙同学 | 甲同学 | ||
骑自行车 | 步行 | 乘公交车 | |
路程 |
|
| |
时间 |
| ||
(2)求乙同学骑自行车的速度.
(3)当甲同学到达学校时,乙同学离学校还有多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克的西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与西瓜的千克数之间的关系如图所示,那么小李赚了( )
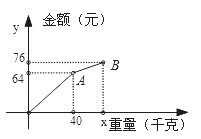
A. 32元B. 36元C. 38元D. 44元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() +
+![]() +2与x轴相交于A,B两点,(点A在B点左侧)与y轴交于点C.
+2与x轴相交于A,B两点,(点A在B点左侧)与y轴交于点C.
(1)求A,B两点坐标.
(2)连结AC,若点P在第一象限的抛物线上,P的横坐标为t,四边形ABPC的面积为S.试用含t的式子表示S,并求t为何值时,S最大.

(3)在(2)的基础上,在整条抛物线上和对称轴上是否分别存在点G和点H,使以A,G,H,P四点构成的四边形为平行四边形?若存在,请直接写出G,H的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com