
【题目】问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
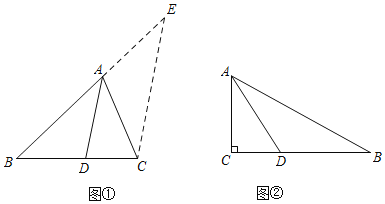
如图①,在△ABC中,AD平分∠BAC交BC于点D,则![]() =
=![]() .提示:过点C作CE∥AD交BA的延长线于点E.
.提示:过点C作CE∥AD交BA的延长线于点E.
请根据上面的提示,写出得到“![]() ”这一结论完整的证明过程.
”这一结论完整的证明过程.
结论应用:如图②,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D.请直接利用“问题探究”的结论,求线段CD的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD,过点A作BC的垂线,垂足为点E,且满足AE=EC,过点C作AB的垂线,垂足为点F,交AE于点G,连接BG.

(1)如图1,若AC=![]() ,CD=4,求BC的长度;
,CD=4,求BC的长度;
(2)如图2取AC上一点Q,连接EQ,在△QEC内取一点,连接QH,EH,过点H作AC的垂线,垂足为点P,若QH=EH,∠QEH=45°.求证:AQ=2HP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1:y=2(x﹣3)2+1和抛物线y2:y=﹣2x2﹣8x﹣3,若无论k取何值,直线y=kx+km+n被两条抛物线所截的两条线段都保持相等,则m=_____,n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点H,点F是![]() 上一点,连接AF交CD的延长线于点E.
上一点,连接AF交CD的延长线于点E.
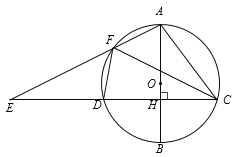
(1)求证:△AFC∽△ACE;
(2)若AC=5,DC=6,当点F为![]() 的中点时,求AF的值.
的中点时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解 在研究函数![]() 的图象性质时,我们用“描点”的方法画出函数的图象.
的图象性质时,我们用“描点”的方法画出函数的图象.
列出表示几组![]() 与
与![]() 的对应值:
的对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点连线:以表中各对对应值为坐标,描出各点,并用平滑的曲线顺次连接这些点,就得到函数![]() 的图象,如图1:
的图象,如图1:
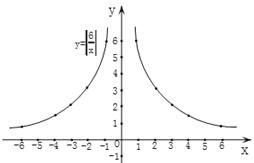
图1
可以看出,这个函数图象的两个分支分别在第一、二象限,且当![]() 时,与函数
时,与函数![]() 在第一象限的图象相同;当
在第一象限的图象相同;当![]() 时,与函数
时,与函数![]() 在第二象限的图象相同.类似地,我们把函数
在第二象限的图象相同.类似地,我们把函数![]() (
(![]() 是常数,
是常数,![]() )的图象称为“并进双曲线”.
)的图象称为“并进双曲线”.
认真观察图表,分别写出“并进双曲线”![]() 的对称性、函数的增减性性质:
的对称性、函数的增减性性质:
①图象的对称性性质: ;
②函数的增减性性质: ;
延伸探究如图2,点M,N分别在“并进双曲线”![]() 的两个分支上,
的两个分支上,![]() ,判断
,判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
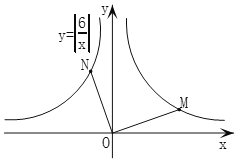
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
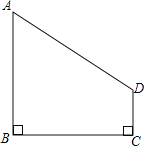
【题目】在四边形ABCD中,∠B=∠C=90°,若AB=4,BC=4,CD=1,问:在BC上是否存在点P,使得AP⊥PD?若存在,求出BP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)从中任取一张,求取到偶数的概率.
(2)甲、乙两人进行摸牌游戏.
①甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
②若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌面倒扣着背面图案相同的四张卡片,其正面分别标记有数字![]() ,先任意抽取一张,卡片上的数记作x,不放回,再抽取一张,卡片上的数字记作y,设点A的坐标为(x,y).
,先任意抽取一张,卡片上的数记作x,不放回,再抽取一张,卡片上的数字记作y,设点A的坐标为(x,y).
(1)用树状图或列表法列举点A所有的坐标情况;
(2)求点A在抛物线![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com