
| 分组 | 划记 | 频数 |
| 60.5~65.5 |  | 2 |
| 65.5~70.5 | 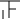 | 4 |
| 70.5~75.5 | 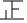 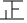 | 10 |
| 75.5~80.5 | 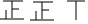 | 12 |
| 80.5~85.5 |  | 8 |
| 85.5~90.5 |  | 6 |
| 90.5~95.5 | 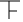 | 3 |
| 合计 |
分析 (1)根据题意填写下面的频数分布表即可;
(2)首先求出及格、良好、优秀所占的百分比,然后画出扇形统计图即可.
解答 解:
| 分组 | 划记 | 频数 |
| 60.5~65.5 |  | 2 |
| 65.5~70.5 | 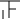 | 4 |
| 70.5~75.5 | 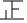 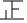 | 10 |
| 75.5~80.5 |  | 12 |
| 80.5~85.5 |  | 8 |
| 85.5~90.5 |  | 6 |
| 90.5~95.5 |  | 3 |
| 合计 |
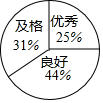
点评 本题考查了扇形统计图,频数(频率)分布表,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
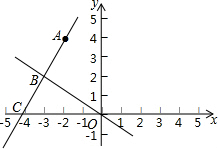 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)
如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
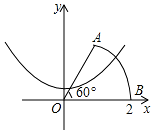 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
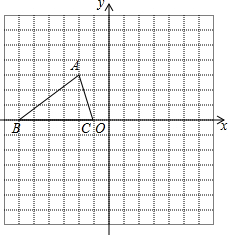 如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
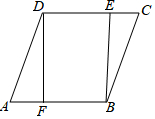 如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com