练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
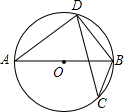
    10．如图，AB是⊙O的直径，CD是⊙O的弦，连接AD、DB、BC，若∠ABD=55°，则∠BCD的度数为（　　）
    A．65°B．55°C．45°D．35°

    分析 先根据圆周角定理求出∠ADB的度数，再由直角三角形的性质求出∠A的度数，进而可得出结论．

    解答 解：∵AB是⊙O的直径，
    ∴∠ADB=90°．
    ∵∠ABD=55°，
    ∴∠A=90°-55°=35°，
    ∴∠BCD=∠A=35°．
    故选D．

    点评 本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

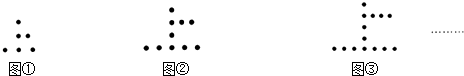
    20．如图，是用棋子摆成的“上”字：如果按照此规律继续摆下去，那么通过观察，可以发现：第10个“上”字需用多少枚棋子（　　）
    A．36B．38C．42D．50

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．先化简，再求值：2x（x-2）-（2x+1）（x-3），其中x=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．李祥用棋子摆出了四个不同的图案（如图），请你仔细观察其中的规律，然后画出按此规律排列的第五个图案，看一看第五个图案中一共有多少个棋子，你能归纳出一个一般性的结论吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求值：（6m-2n）2+（3m+2n）（2m-2n），其中m=-$\frac{1}{3}$，n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列计算正确的是（　　）
    A．2a+3b=5abB．a3•a2=a6C．（a-b）2=a2-b2D．（a2）4=a8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为a1，第二个三角数记为a2，…，第n个三角数记为an，则an-1+an=（　　）（　　）
    A．（n-1）2B．n2C．（n+1）2D．（n+2）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．已知二次函数y=ax2+bx+c的图象与x轴交于点（-2，0），（x，0），且1＜x1＜2，与y轴的正半轴的交点在（0，2）的下方，下列结论正确的是（　　）
    ①4a-2b+c=0
    ②a＜b＜0
    ③2a+c＞0
    ④2a-b+1＞0．
    A．①②③B．②③④C．①③④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．某公司投资40万元生产A，B两种产品．已知投资A产品获得的利润y1（万元）与投资金额x（万元）的关系为y1=x；投资B产品获得的利润y2（万元）与投资金额x（万元）的关系为y2=$\frac{1}{10}$x2，且投资B产品的金额不少于A产品的投资金额．但不多于A产品投资金额的3倍．设投资B产品的金额为x万元．
    （1）若公司计划获得60万元的总利润，求出投资A，B两种产品各多少万元？
    （2）求出公司获得的总利润W（万元）与x的函数关系式，并写出x的取值范围；
    （3）当投资B产品的金额为多少万元时，该公司获得的利润最大，并求出最大利润．

    查看答案和解析>>

    同步练习册答案