
 在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.
在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6. 分析 由MN∥BC可得出∠AMN=∠ABC、∠ANM=∠ACB,进而可得出△AMN∽△ABC,根据相似三角形的性质可得出$\frac{AM}{AB}$=$\frac{MN}{BC}$,代入各边长可求出BC的长.
解答 解:∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴△AMN∽△ABC,
∴$\frac{AM}{AB}$=$\frac{MN}{BC}$,即$\frac{1}{1+3}$=$\frac{\frac{3}{2}}{BC}$,
∴BC=6.
故答案为:6.
点评 本题考查了相似三角形的判定与性质,根据△AMN∽△ABC找出$\frac{AM}{AB}$=$\frac{MN}{BC}$是解题的关键.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:选择题
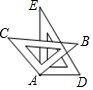 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )| A. | ∠BAD≠∠EAC | B. | ∠DAC-∠BAE=45° | C. | ∠DAC+∠BAE=180° | D. | ∠DAC-∠BAE=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 增加12.25万元 | B. | 减少12.25万元 | C. | 增加12万元 | D. | 减少12万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com