
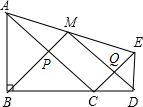
 如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,给出下列结论:
如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,给出下列结论:分析 ①②通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.③根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知,$\frac{AC}{EC}$=$\frac{AB}{ED}$=$\frac{BC}{CD}$;然后由直角三角形中的正切函数,得tan∠AEC=$\frac{AC}{EC}$,再由等量代换求得tan∠AEC=$\frac{BC}{CD}$;④由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答.
解答 解:∵△ABC和△CDE均为等腰直角三角形,
∴AB=BC,CD=DE,
∴∠BAC=∠BCA=∠DCE=∠DEC=45°,
∴∠ACE=90°,
∵△ABC∽△CDE,
∴$\frac{AC}{EC}$=$\frac{AB}{ED}$=$\frac{BC}{CD}$,
①过点M作MN垂直于BD,垂足为N.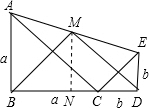
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM≠BC.
故本选项错误;
②又MN=$\frac{1}{2}$(AB+ED)=$\frac{1}{2}$(BC+CD),
∴∠BMD=90°,
即BM⊥DM.
故本选项正确;
③∴tan∠AEC=$\frac{AC}{EC}$,
∴tan∠AEC=$\frac{BC}{CD}$.
故本选项错误;
④∵S△ABC=$\frac{1}{2}$a2,S△CDE=$\frac{1}{2}$b2,S梯形ABDE=$\frac{1}{2}$(a+b)2,
∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,
S△ABC+S△CDE=$\frac{1}{2}$(a2+b2)≥ab(a=b时取等号),
∴S△ABC+S△CDE≥S△ACE.
故本选项正确.
故答案为:②④.
点评 本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点.熟悉锐角三角函数的定义,相似三角形的判定与性质,特别是不等式的基本性质a2+b2≥2ab(a=b时取等号)是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
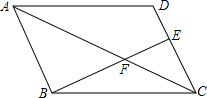 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 4:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
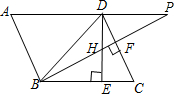 如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:
如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且$\frac{AO}{BO}$=$\frac{1}{\sqrt{5}}$.若点A在y=$\frac{1}{x}$的图象上,则经过点B的反比例函数的解析式是y=-$\frac{5}{x}$.
如图,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且$\frac{AO}{BO}$=$\frac{1}{\sqrt{5}}$.若点A在y=$\frac{1}{x}$的图象上,则经过点B的反比例函数的解析式是y=-$\frac{5}{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com