
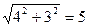
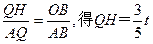
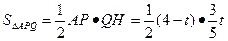
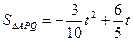 (0<t≤4)
(0<t≤4)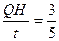

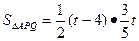
 ··············(4分)
··············(4分)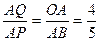
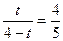 即
即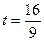
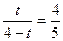 t=-16(舍去)
t=-16(舍去)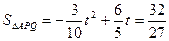 ···············(6分)
···············(6分)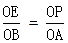
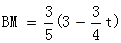
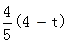
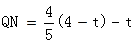 由BM=QN,得
由BM=QN,得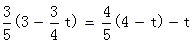
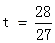 ∴
∴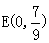 ···································(8分)
···································(8分)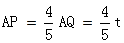
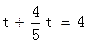
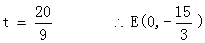 t··············(10分)
t··············(10分)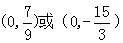
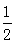 AE
AE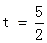 ······················(11分)
······················(11分)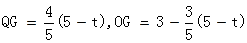
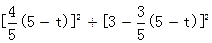




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
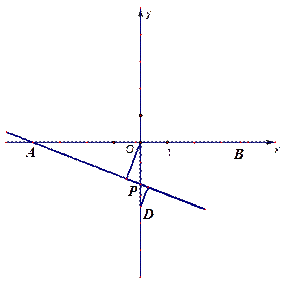
 的值(用含有k的式子表示.);
的值(用含有k的式子表示.); BOM =3S
BOM =3S DOM,且k为方程(k+7)(k+5)-(k+6)(k+5=
DOM,且k为方程(k+7)(k+5)-(k+6)(k+5= 的根,求直线BD的解析式.
的根,求直线BD的解析式. 值不变;②
值不变;② 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值,查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象与
的图象与 轴的交点坐标为(2,0),则下列说法:①
轴的交点坐标为(2,0),则下列说法:① 随
随 的增大而减小;②
的增大而减小;② >0;③关于
>0;③关于 的方程
的方程 的解为
的解为 .其中说法正确的有 (把你认为说法正确的序号都填上).
.其中说法正确的有 (把你认为说法正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 | 甲 | 乙 | 总计 | ||||||
| A | x | | 14 | ||||||
| B | | | 14 | ||||||
| 总计 | 15 | 13 | 28 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

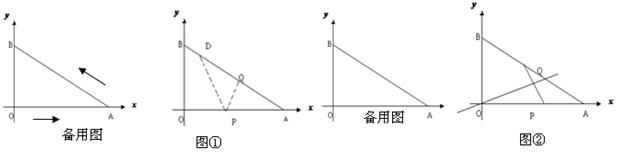
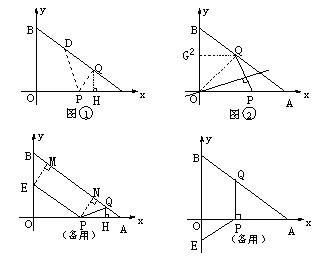
 )上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
)上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com