
分析 由完全平方公式,组中②可变形为(x+2y)2=9,即x+2y=3或x+2y=-3.这样原方程组可变形为关于x、y的两个二元一次方程组,这两个二元一次方程组的解就是原方程组的解.
解答 解:$\left\{\begin{array}{l}{x-3y+2=0①}\\{{x}^{2}+4xy+4{y}^{2}=9②}\end{array}\right.$
由②得:(x+2y)2=9,
即:x+2y=3或x+2y=-3
所以原方程组可化为$\left\{\begin{array}{l}{x-3y=-2}\\{x+2y=3}\end{array}\right.$;$\left\{\begin{array}{l}{x-3y=-2}\\{x+2y=-3}\end{array}\right.$.
解方程组$\left\{\begin{array}{l}{x-3y=-2}\\{x+2y=3}\end{array}\right.$;得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=1}\end{array}\right.$;
解方程组$\left\{\begin{array}{l}{x-3y=-2}\\{x+2y=-3}\end{array}\right.$.得$\left\{\begin{array}{l}{{x}_{2}=-\frac{13}{5}}\\{{y}_{2}=-\frac{1}{5}}\end{array}\right.$.
∴原方程组的解是得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=1}\end{array}\right.$;得$\left\{\begin{array}{l}{{x}_{2}=-\frac{13}{5}}\\{{y}_{2}=-\frac{1}{5}}\end{array}\right.$.
点评 本题考查了二元二次方程组的解法.把二元二次方程组转化为一元一次方程组是解决本题的关键.解决此类问题通常利用公式或因式分解,把其中的一个或两个高次方程降次为一元一次方程,再重新结合得到关于未知数的一元一次方程组.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
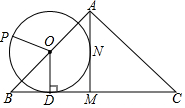 如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.
如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
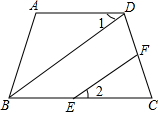 完成下面推理过程.
完成下面推理过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
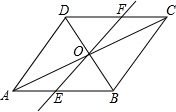 如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接DE、BF
如图,在平行四边形ABCD中,对角线AC与BD交于点O,经过点O的直线交AB于E,交CD于F,连接DE、BF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com