
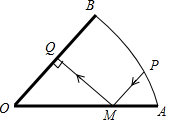
 两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.
两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.分析 (1)根据平面镜反射得到∠BQM=90°,根据平行线的性质,即可得到∠PMQ=90°,进而得出∠OMQ=∠AMP=45°,再根据PM∥OB,即可得到结论;
(2)根据弧长计算公式,即可得到PM的长,再根据△OMQ是等腰直角三角形,即可得到QM的长,进而得到光线从点P射入到返回到点P的总路径的长.
解答 解:(1)∵光线PM经镜面OA反射后射到镜面OB上的点Q,且经镜面OB反射后原路返回,
∴∠BQM=90°,
又∵PM∥OB,
∴∠PMQ=90°,
∴∠OMQ=∠AMP=45°,
∵PM∥OB,
∴∠AOB=∠AMP=45°;
(2)∵OA=OB=10cm,∠AOB=45°,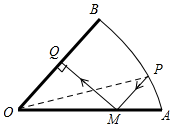
∴$\widehat{AB}$=$\frac{45×π×10}{180}$=$\frac{5}{2}π$,
∵$\widehat{AP}$的度数等于15°,
∴$\widehat{AP}$=$\frac{1}{3}$$\widehat{AB}$=$\frac{5}{6}π$,
即$\frac{45×π×PM}{180}$=$\frac{5}{6}π$,
∴PM=$\frac{10}{3}$=AM,
∴OM=OA-AM=10-$\frac{10}{3}$=$\frac{20}{3}$,
∴QM=OM×sin45°=$\frac{10}{3}\sqrt{2}$,
∴光线从点P射入到返回到点P的总路径的长为2($\frac{10}{3}$+$\frac{10}{3}\sqrt{2}$)=$\frac{20}{3}+\frac{20}{3}\sqrt{2}$.
点评 本题主要考查了平行线的性质以及弧长计算公式,解题时注意:两直线平行,同位角相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.| α | sinα | cosα | tanα |
| 25° | 0.42 | 0.91 | 0.47 |
| 37° | 0.60 | 0.80 | 0.75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com