某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.假设果园增种x棵橙子树,果园橙子的总产量为y个.
(1)求果园增种橙子树x(棵)与果园橙子总产量y(个)的函数关系式.
(2)在上述问题中,果园要种多少棵橙子树,就可以使果园橙子的总产量为最多?
(3)增种多少棵橙子树时,可以使果园橙子的总产量在60420个以上?从计算结果和数学的角度看,你有什么感想(不超过30字)?
解:(1)假设果园增种x棵橙子树,那么果园共有(x+100)棵橙子树,
∵每多种一棵树,平均每棵树就会少结5个橙子,
∴这时平均每棵树就会少结5x个橙子,
则平均每棵树结(600-5x)个橙子.
∵果园橙子的总产量为y,
∴则y=(x+100)(600-5x)
=-5x
2+100x+60000,
(2)∵y=(x+100)(600-5x)
=-5x
2+100x+60000,
∴当x=-

=-
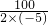
=10(棵),
y
最大=

=65000(个).
故当增种橙树的棵数x取10棵时y的值最大,y的值最大是65000个.
(3)当y=-5x
2+100x+60000=60420时,
整理得出:x
2-20x+84=0,
(x-16)(x-4)=0,
解得:x
1=16,x
2=4,
∵抛物线对称轴为直线x=10,
∴增种5到15棵橙子树时,可以使果园橙子的总产量在60420个以上.
通过以上计算可以发现,果园的树木棵数并不是越多越好,产量的多少取决于科学的计算果树的棵数.
分析:(1)根据题意设多种x棵树,就可求出每棵树的产量,然后求出总产量y与x之间的关系式.
(2)利用当x=-

时,y
最大=

求出即可.
(3)根据函数关系式y=-5x
2+100x+60000=60420,结合一元二次方程解法得出即可.
点评:此题主要考查了二次函数的应用,准确分析题意,列出y与x之间的二次函数关系式是解题关键.

 =-
=-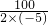 =10(棵),
=10(棵), =65000(个).
=65000(个). 时,y最大=
时,y最大= 求出即可.
求出即可.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案