
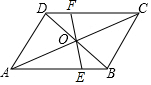
 如图所示,在?ABCD中,EF过对角线AC,BD的交点O,若FC=3DF;S△BOE=2,那么,?ABCD 的面积为32.
如图所示,在?ABCD中,EF过对角线AC,BD的交点O,若FC=3DF;S△BOE=2,那么,?ABCD 的面积为32. 分析 由四边形ABCD是平行四边形,得出∠FDO=∠EBO、OD=OB,由ASA证得△FDO≌△EBO,得出S△DOF=S△BOE,求出S△COD=8即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴∠FDO=∠EBO,OD=OB,
在△FDO和△EBO中,$\left\{\begin{array}{l}{∠FDO=∠EBO}\\{OD=OB}\\{∠FOD=∠EOB}\end{array}\right.$,
∴△FDO≌△EBO(ASA),
∴S△DOF=S△BOE,
∵S△BOE=2,
∴S△DOF=2,
∵FC=3DF,
∴S△COF=6,
∴S△COD=8,
∴?ABCD 的面积=4S△COD=4×8=32,
故答案为:32.
点评 本题主要考查了平行四边形的性质、全等三角形的判定与性质、三角形面积计算、平行四边形面积的计算等知识,熟练掌握全等三角形的面积相等与等高三角形面积计算是解决问题的关键.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
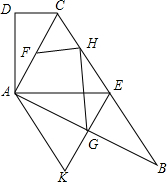 如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.
如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
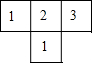 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )| A. |  | B. | 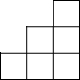 | C. | 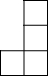 | D. | 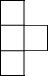 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )
如图,在?ABCD中,对角线AC、BD相交于点O,则下列式子不正确的是( )| A. | BO=OD | B. | AB=CD | C. | ∠BAD=∠BCD | D. | AC=BD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
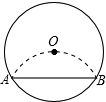 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.| 抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 正面朝上的 频数m | 51 | 98 | 153 | 200 | 250 |
| 正面朝上的 频率mn | 0.51 | 0.49 | 0.51 | 0.50 | 0.51 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com