(1)设(x-3)2+|y+1|=0,求代数式x+y的值;
(2)设a为最小的正整数,b是最大的负整数,c是绝对值最小的数,d是倒数等于本身的有理数,则a+b+c+d=?
(3)已知A=4x2-4xy+y2,B=x2+xy-5y2,求A-B;
(4)(3x2y-2xy2)-(xy2-2x2y),其中x=-1,y=2;
(5)多项式(a-2)x+(2b+1)xy+y3-7是关于x,y的多项式,若该多项式不含二次项和一次项,求3a+2b的值.
解:(1)依题意,得
x-3=0,y+1=0,
解得,x=3,y=-1,
则x+y=3-1=2,即代数式(x+y)的值是2;
(2)根据题意得:a=1,b=-1,c=0,d=±1,则a+b+c+d=±1;
(3)A-B=4x
2-4xy+y
2-x
2-xy+5y
2=3x
2-5xy+6y
2.
(4)(3x
2y-2xy
2)-(xy
2-2x
2y)=3x
2y-2xy
2-xy
2+2x
2y=5x
2y-3xy
2=xy(5x-3y),
把x=-1,y=2代入,得
原式=-2(-5-6)=22;
(5)解:∵多项式(a-2)x+(2b+1)xy+y
3-7是关于x,y的多项式,该多项式不含二次项和一次项,
∴由题意得出:a-2=0,2b+1=0,
解得:a=2,b=-

,
∴3a+2b=3×2+2×(-

)=6-1=5.
分析:(1)根据非负数的性质求得x、y的值,然后求得代数式x+y的值;
(2)根据最小的正整数为1,最大的负整数为-1,绝对值最小的有理数为0,以及倒数等于本身的数为1或-1,确定出a,b,c,d的值,即可求出a+b+c+d的值;
(3)把A、B的值代入(A-B),然后合并同类项;
(4)先化简,然后代入求值;
(5)根据多项式中不含二次项和一次项得出a-2=0,2b+1=0,求出a,b的值,求出3a+2b的值即可.
点评:本题综合考查了整式的加减、多项式以及多项式求值等知识点.代数式的求值:求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.

 ,
, )=6-1=5.
)=6-1=5.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 已知⊙O1的半径为R,周长为C.
已知⊙O1的半径为R,周长为C.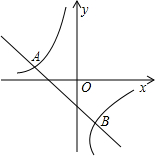 如图,若反比例函数y=-
如图,若反比例函数y=-