【题目】若(x+2y)(2x-ky-1)的结果中不含xy项，则k的值为（ ）
A. 4 B. -4 C. 2 D. -2
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】解答
（1）已知，如图①，在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE=BD+CE．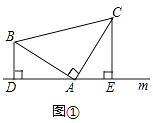 
（2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意钝角，请问结论DE=BD+CE是否成立？若成立，请你给出证明：若不成立，请说明理由．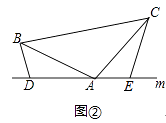 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，直线y=kx+2与x轴、y轴分别交于点A(-1,0)和点B，与反比例函数y=
的图象在第一象限内交于点C（1，n）．
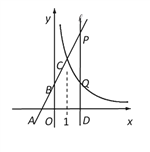
（1）求k的值；
（2）求反比例函数的解析式；
（3）过x轴上的点D（a，0）作平行于y轴的直线
（a＞1），分别与直线AB和双曲线
交于点P、Q，且PQ=2QD，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′ ，如图①所示，∠BAB′ ＝θ， 
，我们将这种变换记为[θ，n] ．
（1）如图①，对△ABC作变换[60°，
]得到△AB′C′ ，则
:
= ；直线BC与直线B′C′所夹的锐角为 度；
（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、
在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；
（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=mx+4的图象与x轴相交于点A，与反比例函数y=
的图象相交于点B（1，6）．
（1）求一次函数和反比例函数的解析式；
（2）设点P是x轴上一点，若S△APB=18，直接写出点P的坐标．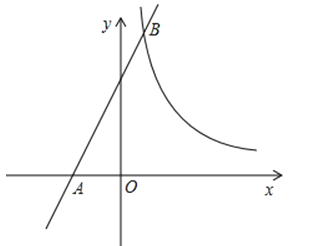
查看答案和解析>>
科目：初中数学 来源： 题型：
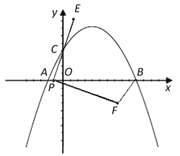
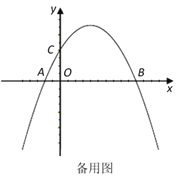
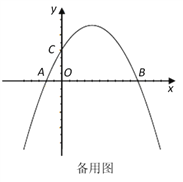
【题目】如图，在平面直角坐标系中，已知点A、B、C的坐标分别为(-1，0)，(5，0)，(0，2)．
（1）求过A、B、C三点的抛物线解析式；
（2）若点P从A点出发，沿x轴正方向以每秒1个单位长度的速度向B点移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF，连接FB．若点P运动的时间为t秒(0≤t≤6)，设△PBF的面积为S；
①求S与t的函数关系式；
②当t是多少时，△PBF的面积最大，最大面积是多少？
（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】反比例函数y=
的图象如图所示，以下结论：
①常数m＜﹣1；
②在每个象限内，y随x的增大而增大；
③若点A（﹣1，h），B（2，k）在图象上，则h＜k；
④若点P（x，y）在上，则点P′（﹣x，﹣y）也在图象．
其中正确结论的个数是（ ）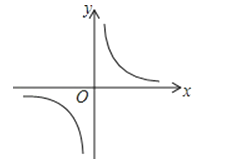
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）为举办校园文化艺术节，甲、乙两班准备给合唱同学购买演出服装（一人一套），两班共92人（其中甲班比乙班人多，且甲班不到90人），下面是供货商给出的演出服装的价格表：
如果两班单独给每位同学购买一套服装，那么一共应付5020元．
（1）甲、乙两班联合起来给每位同学购买一套服装，比单独购买可以节省多少钱？
（2）甲、乙两班各有多少名同学？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
