
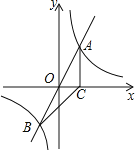
【题目】如图, 正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
【答案】(1)k=2(2)D(![]() ,0)或(-
,0)或(-![]() ,0)
,0)
【解析】试题分析:(1)根据对称性可得OA=OB,从而可得△ACO的面积为1,由此可求出点A的坐标,然后运用待定系数法就可解决问题,
(2)先将y=2x与y=![]() 联立成方程组,求出A,B两点的坐标,由 O为线段AB的中点,
联立成方程组,求出A,B两点的坐标,由 O为线段AB的中点,
可得OD=![]() AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
试题解析:(1)设点A的坐标为(m,n),
∵点A在直线y=2x上,
∴n=2m,
根据对称性可得OA=OB,
∴S△ABC=2S△ACO=2,
∴S△ACO=1,
∴![]() m2m=1,
m2m=1,
∴m=1(舍负),
∴点A的坐标为(1,2),
∴k=1×2=2,
(2)x轴上存在一点D,使△ABD为直角三角形,
将y=2x与y=![]() 联立成方程组得:
联立成方程组得:
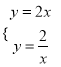 ,
,
解得: ![]() ,
,![]() ,
,
∴A(1,2),B(-1,-2),
当AD⊥BD时,如图,
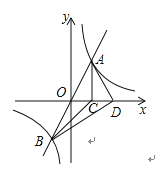
∵O为线段AB的中点,
∴OD=![]() AB=OA,
AB=OA,
∵A(1,2),
∴OC=1,AC=2,
由勾股定理得:OA=![]() =
=![]() ,
,
∴OD=![]() ,
,
∴D(![]() ,0),
,0),
根据对称性,当D为直角顶点,且D在x轴负半轴时,D(-![]() ,0),
,0),
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小明在解方程组![]() 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:![]() 请你解决以下问题:
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组![]()
(2)已知 x、y、z,满足![]() 试求 z 的值.
试求 z 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
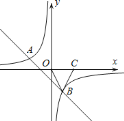
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
![]() Ⅰ
Ⅰ![]() 试确定上述反比例函数和一次函数的表达式;
试确定上述反比例函数和一次函数的表达式;
![]() Ⅱ
Ⅱ![]() 连OB,在x轴上取点C,使
连OB,在x轴上取点C,使![]() ,并求
,并求![]() 的面积;
的面积;
![]() Ⅲ
Ⅲ![]() 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC底边BC的长为4cm,面积为12cm,腰AB的垂直平分线交AB于点E,若点D为BC边的中点,M为线段EF上一动点,则△BDM的周长最小值为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=90,A是∠MON内部的一点,过点A作AB⊥ON,垂点为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动。设运动时间为t秒(t>0)。
(1)当t=1秒时,ΔEOF与ΔABO是否相似?请说明理由。
(2)在运动过程中,不论t取何值时,总有EF⊥OA,为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得SΔAEF=![]() S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
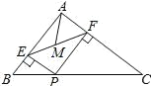
A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
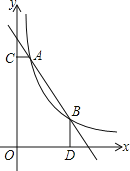
【题目】如图,一次函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 轴于C,
轴于C,![]() 轴于D
轴于D
![]() 求k的值;
求k的值;
![]() 根据图象直接写出
根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
![]() 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若![]() 和
和![]() 面积相等,求点P坐标.
面积相等,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
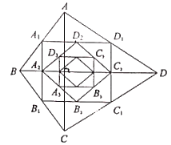
【题目】如图,四边形![]() 中,
中,![]() 顺次连接四边形
顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ,再顺次连接四边形
,再顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ...如此进行下去,得到四边形
...如此进行下去,得到四边形![]() 则下列结论正确的个数有( )
则下列结论正确的个数有( )
①四边形![]() 是矩形;②四边形
是矩形;②四边形![]() 是菱形;③四边形
是菱形;③四边形![]() 的周长为
的周长为![]() ; ④四边形
; ④四边形![]() 的面积是
的面积是![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com