
分析 利用平方差公式以及立方差公式,将a-b、a$\sqrt{a}$-b$\sqrt{b}$展开,再消元合并同类二次根式即可.
解答 解:原式=$\frac{(\sqrt{a})^{2}-(\sqrt{b})^{2}}{\sqrt{a}-\sqrt{b}}$-$\frac{(\sqrt{a})^{3}-(\sqrt{b})^{3}}{(\sqrt{a})^{2}+\sqrt{a}\sqrt{b}+(\sqrt{b})^{2}}$,
=$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{\sqrt{a}-\sqrt{b}}$-$\frac{(\sqrt{a}-\sqrt{b})[(\sqrt{a})^{2}+\sqrt{a}\sqrt{b}+(\sqrt{b})^{2}]}{(\sqrt{a})^{2}+\sqrt{a}\sqrt{b}+(\sqrt{b})^{2}}$,
=$\sqrt{a}$+$\sqrt{b}$-($\sqrt{a}$-$\sqrt{b}$),
=2$\sqrt{b}$.
点评 本题考查了二次根式的混合运算,熟记平方差与立方差公式是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
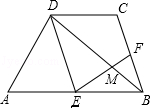 如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
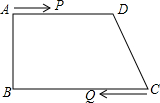 如图,梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从点A开始,沿AD边,以1厘米/秒的速度向点D运动;动点Q从点C开始,沿CB边,以3厘米/秒的速度向B点运动.已知P、Q两点分别从A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.假设运动时间为t秒,问:
如图,梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从点A开始,沿AD边,以1厘米/秒的速度向点D运动;动点Q从点C开始,沿CB边,以3厘米/秒的速度向B点运动.已知P、Q两点分别从A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.假设运动时间为t秒,问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com