证明:(1)AD是△ABC的中线(已知),
∴BD=CD.
在Rt△EBD和Rt△FCD中,

∴Rt△EBD≌Rt△FCD(HL).
∴DE=DF(全等三角形的对应边相等),
即AD是∠BAC的平分线.
(2)在Rt△AED和Rt△AFD中,
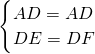
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF(全等三角形的对应边相等).
又∵BE=CF(已知),
∴AB=AC.
分析:(1)要证AD平分∠BAC,只需证明△ABD≌△ACD即可.
(2)由1可证得Rt△AED≌Rt△AFD,然后推出BE=CF可得AB=AC.
点评:本题考查了全等三角形的判定和性质;三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

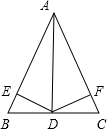 已知:如图所示,AD是△ABC的中线,DE⊥AB于E,DF⊥AC于F且BE=CF.
已知:如图所示,AD是△ABC的中线,DE⊥AB于E,DF⊥AC于F且BE=CF.
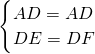 ,
,
