练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．抛物线过（-1，10）、（1，4）、（2，7）三点，求抛物线的解析式．

    分析 直接将三点代入函数关系式，进而得出方程组，求出答案即可．

    解答 解：设抛物线解析式为：y=ax2+bx+c，
    将（-1，10）、（1，4）、（2，7）三点分别代入得：
    $\left\{\begin{array}{l}{a-b+c=10}\\{a+b+c=4}\\{4a+2b+c=7}\end{array}\right.$，
    解得：$\left\{\begin{array}{l}{a=2}\\{b=-3}\\{c=5}\end{array}\right.$，
    故抛物线的解析式为：y=2x2-3x+5．

    点评 此题主要考查了待定系数法求二次函数关系式，正确解方程组是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

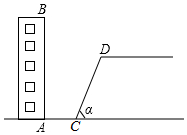    16．如图，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°，根据有关部门的规定，∠α≤39°时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？（结果取整数）
    （参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81，$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{5}$≈2.24）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某房地产开发公司计划建A、B两种户型的住房共80套，A种户型每套成本和售价分别为90万元和102万元，B种户型每套成本和售价分别为60万元和70万元．设计划建A户型x套，所建户型全部售出后获得的总利润为W万元．
    【思考】
    （1）根据所给条件，完成下表：
    A户型B户型
    套数x80-x
    利润（万元）12x10（80-x）
    （2）求W与x之间的函数解析式；
    【探究】
    （3）该公司所建房资金不少于5700万元，且所筹资金全部用于建房，若A户型不超过32套，则该公司有哪几种建房方案？
    （4）在（3）的前提下，根据国家房地产政策，公司计划每套A户型住房的售价降低a万元（0＜a≤3），B户型住房的售价不变，且预计所建的两种住房全部售出，求该公司获得最大利润的方案．
    【决策】
    为了适应市场需要，该公司在总套数不变的情况下，改建若干套C户型，现已知C户型每套成本110万元，售价118万元．若该公司所筹资金为6300万元且刚好用完，则当x=45套时，该公司所建房售出后获得的总利润最大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

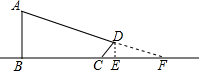    9．小明在某一时刻测得1m的杆子在阳光下的影子长为2m，他想测量电线杆AB的高度，但其影子恰好落在土坡的坡面CD和地面BC上，量得CD=4m，BC=10m，CD与底面成45°，求电线杆的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

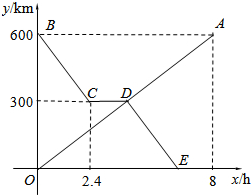    16．货车和轿车分别从甲、乙两地同时出发，沿同一公路相向而行．轿车出发3h后休息，直至与货车相遇后，以原速度继续行驶．设货车出发xh后，货车、轿车分别到达离甲地y1km和y2km的地方，图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系．
    （1）求点D的坐标，并解释点D的实际意义；
    （2）求线段DE所在直线的函数表达式；
    （3）当货车出发$\frac{10}{3}$或5h时，两车相距50km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知抛物线y=x2-2x-a．
    （1）若抛物线与x轴有两个交点，求a的取值范围；
    （2）当代数式x2-2x-1的值为负整数时，求x的值．
    （3）设抛物线与y轴的交点为A，顶点为B，直线AB与x轴交于点C，抛物线与x轴的右交点为D，是否存在C，D两点关于y轴对称的情况？如果存在，求出此时a的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

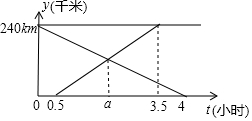    13．甲、乙两车分别从A、B两地相向而行，甲车出发0.5小时后乙车出发，并以各自速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是两车离B地距离y与甲车出发时间t（小时）之间的函数图象．
    （1）a=2；
    （2）若甲乙两车之间的距离s（米），则s与甲车出发时间t≥a之间的函数关系式为：s=$\left\{\begin{array}{l}{140t-280（2≤t≤3.5）}\\{60t（3.5＜t≤4）}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

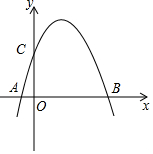    10．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（-1，0），B（3，0），C（0，3）三点，O为坐标原点．
    （1）求此抛物线的解析式；
    （2）若将此抛物线向下平移h个单位长度，使平移后的抛物线顶点落在Rt△BOC内（包括△BOC边界），求h的范围；
    （3）试问在y轴上是否存在一点P，使∠OPA+∠OCA=∠CBA？若存在，求出CP之长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．一手机经销商计划购进某品牌的A型、B型两款手机共40部，每款手机至少要购进10部，设购进A型手机x部，B型手机y部，两款手机的金价和预售价如表：
    手机型号A型B型
    进价（单位：元/部）9001200
    预售价（单位：元/部）12001600
    （1）求出y与x之间的函数关系式；
    （3）假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．
    ①求出预估利润P（元）与x（部）的函数关系式；
    ②求出预估利润的最大值，并写出此时购进两款手机各多少部．

    查看答案和解析>>

    同步练习册答案