
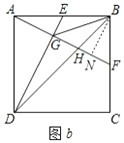
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 交于点
交于点![]() .
.
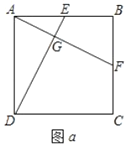
(1)求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
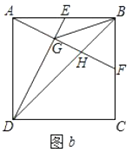
①求证:![]() ;
;
②若![]() ,求三角形
,求三角形![]() 的面积.
的面积.
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
(1)由正方形的性质可得AD=BC=DC=AB,AE=BE=![]() AB,BF=CF=
AB,BF=CF=![]() BC,由SAS可证△ADE≌△BAF,可得∠BAF=∠ADE,由余角的性质可得结论;
BC,由SAS可证△ADE≌△BAF,可得∠BAF=∠ADE,由余角的性质可得结论;
(2)①过点B作BN⊥AF于N,由AAS可证△ABN≌△ADG,可得AG=BN,DG=GN,由平行线分线段成比例可得AG=GN,由勾股定理可得结论;
②由勾股定理可求DE的长,由面积法可求AG的长,由相似三角形的性质可求GH的长,由三角形的面积可求解.
解:(1)证明:∵正方形![]() ,
,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵在△ADE和△BAF中,
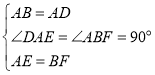 ,
,
∴△ADE和△BAF(SAS),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)证明:①如图![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
在△ABN和△ADG中,
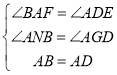 ,
,
∴△ABN和△ADG(AAS),
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
且![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】将一副三角尺按如图①方式拼接:含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合(在Rt△ABC中,∠ACB=90°,∠BAC=30°;在Rt△ACD中,∠ADC=90°∠DAC=45°)已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当PD=BC时,求∠PDA的度数;
(2)如图②,若E是CD的中点,求△DEP周长的最小值;
(3)如图③,当DP平分∠ADC时,在△ABC内存在一点Q,使得∠DQC=∠DPC,且CQ=![]() ,求PQ的长.
,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
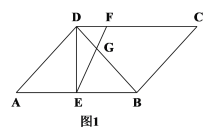
【题目】在平行四边形ABCD中,AD=BD,E为AB的中点,F为CD上一点,连接EF交BD于G.
(1)如图1,若DF=DG=2,AB=8,求EF的长;
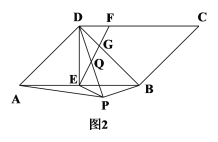
(2)如图2,∠ADB=90°,点P为平行四边形ABCD外部一点,且AP=AD,连接BP、DP、EP,DP交EF于点Q,若BP⊥DP,EF⊥EP,求证:DQ=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
(2)如图2,P是BC边上一点,∠BAP=∠C,tan∠PAC=![]() ,BP=2cm,求CP的长.
,BP=2cm,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知正比例函数
中,已知正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
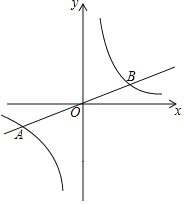
(1)反比例函数的解析式为____________,点![]() 的坐标为___________;
的坐标为___________;
(2)观察图像,直接写出![]() 的解集;
的解集;
(3)![]() 是第一象限内反比例函数的图象上一点,过点
是第一象限内反比例函数的图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为3,求点
的面积为3,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“村村通公路政策,是近年来国家构建和谐社会,支持新农村建设的一项重大公共决策,是一项民心工程,惠民工程某镇政府准备向甲、乙两个工程队发包一段“村村通”工程建设项目,经调查:甲、乙两队单独完成该工程,乙队所需时间是甲队的2倍;甲、乙两队共同完成该工程需30天;若甲队每天所需劳务费用为2400元,乙队每天所需劳务费用为1500元,从节约资金的角度考虑,应选择哪个工程队更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
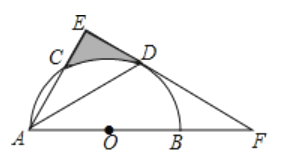
(1)求证:EF为半圆O的切线.
(2)若AO=BF=2,求阴影区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现,每月销售的数量y(件)是售价x(元/件)的一次函数,其对应关系如表:
x/(元/件) | 22 | 25 | 30 | 35 | … |
y/件 | 280 | 250 | 200 | 150 | … |
在销售过程中销售单价不低于成本价,物价局规定每件商品的利润不得高于成本价的60%,
(1)请求出y关于x的函数关系式.
(2)设小明每月获得利润为w(元),求每月获得利润w(元)与售价x(元/件)之间的函数关系式,并确定自变量x的取值范围.
(3)当售价定为多少元/件时,每月可获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com