
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线与x轴交于点P,若△ABP的面积为![]() ,试求点P的坐标.
,试求点P的坐标.

【答案】(1)A(﹣![]() ,0);(2)P点坐标为(1,0)或(﹣4,0)
,0);(2)P点坐标为(1,0)或(﹣4,0)
【解析】
试题(1)把x=0,y=0分别代入函数解析式,即可求得相应的y、x的值,则易得点A、B的坐标;
(2)由B、A的坐标易求:OB=3,OA=![]() .然后由三角形面积公式得到S△ABP=
.然后由三角形面积公式得到S△ABP=![]() APOB=
APOB=![]() ,则AP=
,则AP=![]() .设点P的坐标为(m,0),则m﹣(﹣
.设点P的坐标为(m,0),则m﹣(﹣![]() )=
)=![]() 或﹣
或﹣![]() ﹣m=
﹣m=![]() ,由此可以求得m的值.
,由此可以求得m的值.
试题解析:(1)由x=得:y=3,即:B(0,3).
由y=0得:2x+3=0,解得:x=﹣![]() ,即:A(﹣
,即:A(﹣![]() ,0);
,0);
(2)由B(0,3)、A(﹣![]() ,0)得:OB=3,OA=
,0)得:OB=3,OA=![]()
∵S△ABP=![]() APOB=
APOB=![]()
∴![]() AP=
AP=![]() ,
,
解得:AP=![]() .
.
设点P的坐标为(m,0),则m﹣(﹣![]() )=
)=![]() 或﹣
或﹣![]() ﹣m=
﹣m=![]() ,
,
解得:m=1或﹣4,
∴P点坐标为(1,0)或(﹣4,0).
 .
.


科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹,下面是甲、乙两人各自的射击情况记录(其中乙的情况记录表上射中9,10环的子弹数因被墨水污染而看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发):
甲

乙

(1)求甲同学在这次测验中平均每发射中的环数;
(2)根据这次测验的情况,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.(结果保留到小数点后1位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强居民节约用水意识,某市在2018年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:

某户居民四月份用水10 m3时,缴纳水费23元.
(1) 求a的值;
(2) 若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧 ![]() 上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是 .
上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC=________.
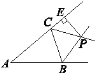
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4. 
(1)求抛物线的表达式;
(2)抛物线上有两点M(x1 , y1)和N(x2 , y2),若x1<1,x2>1,x1+x2>2,试判断y1与y2的大小,并说明理由;
(3)直线l过A及C(0,﹣2),P为抛物线上一点(在x轴上方),过P作PD∥y轴交直线AC于点D,以PD为直径作⊙E,求⊙E在直线AC上截得的线段的最大长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,D是AB边上的一点,过点D作DE∥BC,∠ABC的角平分线于点E.
(1)如图1,当点E恰好在AC边上时,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,其余条件不变,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由。
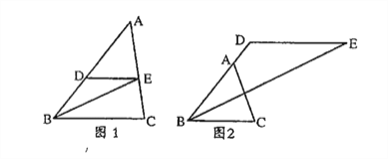
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com