
【题目】如图,反比例函数![]() 与正比例函数y=ax相交于A(1,k),B(-k,-1)两点。
与正比例函数y=ax相交于A(1,k),B(-k,-1)两点。
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数![]() 的图象交于C(x1,y1)、D(x2,y2),且|x1-x2|·|y1-y2|=5,求b的值。
的图象交于C(x1,y1)、D(x2,y2),且|x1-x2|·|y1-y2|=5,求b的值。

【答案】(1)反比例函数解析式为y=![]() ,正比例函数的解析式为y=x;
,正比例函数的解析式为y=x;
(2)b的值为±1.
【解析】试题分析:(1)根据点A与点B关于原点对称,可以求出k的值,将点A分别代入反比例函数与正比例函数的解析式,即可得解;(2)分别把点(x1,y1)、(x2,y2)代入一次函数y=x+b,再把两式相减,根据|x1-x2||y1-y2|=5得出|x1-x2|=|y1-y2|=![]() ,然后通过联立方程求得x1、x2的值,代入即可求得b的值.
,然后通过联立方程求得x1、x2的值,代入即可求得b的值.
试题解析:
(1)据题意得:点A(1,k)与点B(-k,-1)关于原点对称,
∴k=1,
∴A(1,1),B(-1,-1),
∴反比例函数和正比例函数的解析式分别为y=![]() ,y=x;
,y=x;
(2)∵一次函数y=x+b的图象过点(x1,y1)、(x2,y2),
∴![]() ,②-①得,y2-y1=x2-x1,
,②-①得,y2-y1=x2-x1,
∵|x1-x2|·|y1-y2|=5,
∴|x1-x2|=|y1-y2|=![]() ,
,
由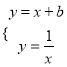 得x2+bx-1=0,
得x2+bx-1=0,
解得,x1=![]() ,x2=
,x2=![]() ,
,
∴|x1-x2|=|![]() -
- ![]() |=|
|=|![]() |=
|=![]() ,
,
解得b=±1.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(2,3),则点B(﹣4,﹣1)的对应点D的坐标为( )
A. (﹣7,﹣2) B. (﹣7,0) C. (﹣1,﹣2) D. (﹣1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.
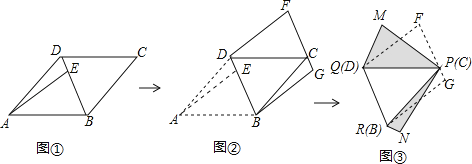
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断正误,并说明理由
(1)给定一组数据,那么这组数据的众数有可能不唯一;理由
(2)给定一组数据,那么这组数据的平均数一定是这组数据中的一个数;
理由
(3)n个数的中位数一定是这n个数中的某一个;理由
(4)求9个数据(x1、x2、……、x9 , 其平均数为m)的标准差S, 计算公式为: ![]() ;理由
;理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.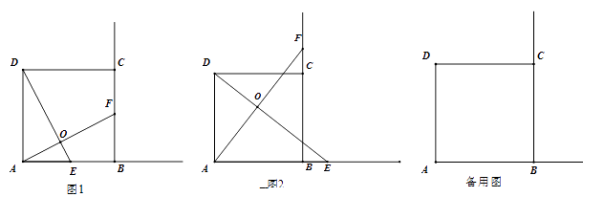
(1)如图1,当点E、F分别在线段AB、BC上时,则线段DE与线段AF的数量关系是 , 位置关系是.
(2)将线段AE沿AF进行平移至FG,连结DG.
①如图2,当点E在AB延长线上时,补全图形,写出AD,AE,DG之间的数量关系.
②若DG= ![]() ,
, ![]() ,直接写出AD长。
,直接写出AD长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”促销期间规定:超市内所有商品按标价的![]() 出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额 |
|
|
|
获得奖券金额(元) |
|
|
|
(符号![]() 表示
表示![]() 是大于或等于
是大于或等于![]() ,而小于
,而小于![]() 的数)
的数)
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额![]() 商品的折扣
商品的折扣![]() 相应的奖券金额,例如:购买标价为
相应的奖券金额,例如:购买标价为![]() 元的商品,则消费金额为:
元的商品,则消费金额为: ![]() 元,获得的优惠额为:
元,获得的优惠额为: ![]() 元.
元.
(![]() )购买一件标价为
)购买一件标价为![]() 元的商品,求获得的优惠额.
元的商品,求获得的优惠额.
(![]() )对于标价在
)对于标价在![]() 元与
元与![]() 元之间(含
元之间(含![]() 元和
元和![]() 元)的商品,顾客购买标价为多少元的商品时可以得到
元)的商品,顾客购买标价为多少元的商品时可以得到![]() 的优惠率.(设购买该商品得到的优惠率
的优惠率.(设购买该商品得到的优惠率![]() 购买商品获得的优惠额
购买商品获得的优惠额![]() 商品的标价)
商品的标价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com