
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).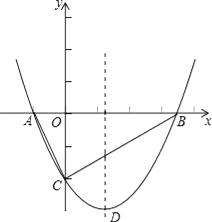
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
【答案】
(1)解:∵点A(-1,0)在抛物线y= ![]() x2 + bx-2上,
x2 + bx-2上,
∴ ![]() × (-1 )2 + b× (-1)–2 = 0,
× (-1 )2 + b× (-1)–2 = 0,
解得b= ![]() ,
,
∴ 抛物线的解析式为y= ![]() x2-
x2- ![]() x-2.
x-2.
y= ( x2 -3x- 4 ) = ![]() (x-)2-
(x-)2- ![]() ,
,
∴顶点D的坐标为 ( ![]() ,-
,- ![]() ).
).
(2)解:当x = 0时y = -2,
∴C(0,-2),OC = 2。
当y = 0时, ![]() x2-
x2- ![]() x-2 = 0,
x-2 = 0,
∴x1 =-1, x2 = 4,
∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2.
∴△ABC是直角三角形.
(3)解:作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,设M点(m,0)则OM=m,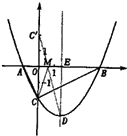
根据轴对称性及两点之间线段最短可知,MC + MD的值最小及△DCM的周长最小
设抛物线的对称轴交x轴于点E.则E点(![]() ,0),
,0),
∴ME=![]() -m, ED=
-m, ED=![]() ;
;
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴ ![]()
∴ ![]() , ∴m =
, ∴m = ![]() .
.
所以M的坐标为( ![]() ,0)
,0)
【解析】( 1)将A点的坐标代入函数解析式y= ![]() x2 + bx-2,得出一个关于b的一元一次方程,求解得出b的值,从而得出二次函数的解析式,然后用配方法将函数解析式陪成顶点式,从而得出顶点D的坐标 ;
x2 + bx-2,得出一个关于b的一元一次方程,求解得出b的值,从而得出二次函数的解析式,然后用配方法将函数解析式陪成顶点式,从而得出顶点D的坐标 ;
(2)首先根据抛物线与坐标轴交点的坐标特点得出C,B两点的坐标,从而得出OC,OA,OB,AB的长度,根据勾股定理的逆定理判断出△ABC是直角三角形.;
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,设M点(m,0)则OM=m,根据轴对称性及两点之间线段最短可知,MC + MD的值最小及△DCM的周长最小 ,设抛物线的对称轴交x轴于点E..则E点(![]() ,0) ,从而得出ME=
,0) ,从而得出ME=![]() -m, ED=
-m, ED=![]() ; 由于ED∥y轴,根据平行于三角形一边的直线,截其它两边的延长线,所截得的三角形与原三角形相似得出△C′OM∽△DEM.根据相似三角形对应边成比例得出OM∶EM=OC'∶ED ,从而得出一个关于m的一元一次方程,求解得出m的值,从而得出M点的坐标 。
; 由于ED∥y轴,根据平行于三角形一边的直线,截其它两边的延长线,所截得的三角形与原三角形相似得出△C′OM∽△DEM.根据相似三角形对应边成比例得出OM∶EM=OC'∶ED ,从而得出一个关于m的一元一次方程,求解得出m的值,从而得出M点的坐标 。


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
A.200 ![]()
B.200
C.100 ![]()
D.100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 OACB 的顶点 O、A、B 的坐标分别是(0,a)、(b,0),且a、b 满足![]()
![]()
![]() b .
b .
(1)如图 1,a= ,b= ,点 C 的坐标 .
(2)如图 2,点 P 为边 OB 上一动点,将线段 AP 绕 P 点顺时针旋转 90°至 PD.当点 P 从O 运动到 B 的过程中,求点 D 运动路径的长度.
(3)如图 3,在(2)的条件下,作等腰 Rt△BED,且∠DBE=90°,再作等腰 Rt△ECF, 且∠ECF=90°,直线 FE 分别交 AC、OB 于点 M、N,求证:FM=EN.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
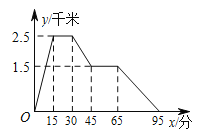
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.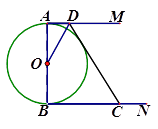
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个运输队承包了一家公司运送货物的业务,第一次运送18吨,派了1辆大卡车和5辆小卡车;第二次运送38吨,派了2辆大卡车和11辆小卡车,并且两次派的车都刚好装满。
(1)两种车型的载重量各是多少吨?
(2)若大卡车运送一次的费用为200元,小卡车运送一次的费用为60元,在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE中.
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com