
 如图,抛物线y=ax2+bx+2与坐标轴交于A、B、C三点,其中B(4,0)、C(-2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
如图,抛物线y=ax2+bx+2与坐标轴交于A、B、C三点,其中B(4,0)、C(-2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.分析 (1)根据B,C两点在抛物线y=ax2+bx+2上,代入抛物线得到方程组,求出a,b的值,即可解答;
(2)先求出直线AB的解析式为y=-$\frac{1}{2}$x+2,设F点的坐标为(x,$-\frac{1}{2}$x+2),则D点的坐标为(x,$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$),根据G点与D点关于F点对称,所以G点的坐标为(x,$\frac{1}{4}{x}^{2}-\frac{3}{2}x+2$),若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,分两种情况解答:①若⊙G与x轴相切则必须由DG=GE;②若⊙G与y轴相切则必须由DG=OE;
(3)M点的横坐标为2±2$\sqrt{2}$,N点的横坐标为$\frac{8}{3}$±2$\sqrt{2}$.
解答 解:(1)∵B,C两点在抛物线y=ax2+bx+2上,
∴$\left\{\begin{array}{l}{16a+4b+2=0}\\{4a-2b+2=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{1}{2}}\end{array}\right.$.
∴所求的抛物线为:y=$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$.
(2)抛物线y=$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$,则点A的坐标为(0,2),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=2}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$.
∴直线AB的解析式为y=-$\frac{1}{2}$x+2,
设F点的坐标为(x,$-\frac{1}{2}$x+2),则D点的坐标为(x,$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2$),
∵G点与D点关于F点对称,
∴G点的坐标为(x,$\frac{1}{4}{x}^{2}-\frac{3}{2}x+2$),
若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,
①若⊙G与x轴相切则必须由DG=GE,
即-$\frac{1}{4}$x2+$\frac{1}{2}$x+2-($\frac{1}{4}{x}^{2}-\frac{3}{2}x+2$)=$\frac{1}{4}{x}^{2}-\frac{3}{2}x+2$,
解得:x=$\frac{2}{3}$,x=4(舍去);
②若⊙G与y轴相切则必须由DG=OE,
即$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+2-(\frac{1}{4}{x}^{2}-\frac{3}{2}x+2)=x$
解得:x=2,x=0(舍去).
综上,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,G点的横坐标为2或$\frac{2}{3}$.
(3)M点的横坐标为2±2$\sqrt{2}$,N点的横坐标为$\frac{8}{3}$±2$\sqrt{2}$.
点评 本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式,难度较大,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
| 销售方式 | 直接出售 | 加工成罐头销售 |
| 利润(元/千克) | 4 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是( )
为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是( )| A. | 100人 | B. | 200人 | C. | 260人 | D. | 400人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
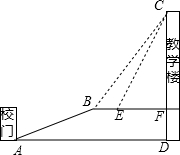 重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com