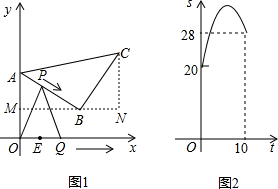
解:(1)过点B作BM⊥y轴于点M,过点C作CN⊥MB的延长线于点N,
∴∠AMB=∠CNB=90°
∵点A,B的坐标分别为(0,10),(8,4),
∴MB=8,MO=4,AO=10,
∴AM=6,在Rt△AMB中,由勾股定理,得
AB=10
∵△ABC是等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴△AMB≌△BNC,
∴BN=AM=6,CN=BM=8,
∴MN=14,CN=8
∴C(14,12)
(2)由图2可知,点P从A运动到B用了10秒
∵AB=10,10÷10=1,
∴P,Q两点运动速度均为每秒1个单位.
(3)作PG⊥y轴于G,BF⊥y轴于F,如图则PG∥BF,
∴△AGP∽△AFB,
∴
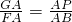
,
∴GA=

t,
∴OG=10-

t,
∵OQ=4+t,
∴S=

OQ×OG=

(4+t)( 10-

t)
即S=-
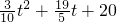
S=-

(t
2-

t)+20
S=-

(t-

)
2+
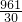
∴当t=

时,S有最大值,此时,GP=
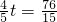
,OG=10-

t=
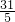
∴P(
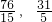
)
(4)当P在AB 上时,若OP=PQ如图则作PH⊥x轴,
于是OH=

OQ=
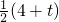
.
∵△AGP∽△AFB
∴
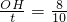
,OH=
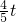
∴
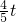
=
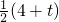
,t=

当P在 BC上时,若OP=PQ
过P作PH⊥x轴,过B作BF⊥y轴于F,交PH于M.
∵△PBM∽△BAF,OH=

OQ=
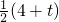
,PB=t-10,BA=10,AF=6,
∴
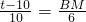
,BM=

(t-10),
∴8+

(t-10)=
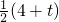
,t=0(舍去),
∴综上所述:当t=

时,OP=PQ
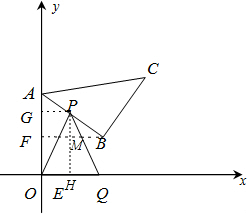
分析:(1)过点B作BM⊥y轴于点M,过点C作CN⊥MB的延长线于点N,由条件可以得出△AMB≌△BNC,根据A、B的坐标可以求出AM、BM的值,可以求出C的坐标,由勾股定理可以求出AB的值.
(2)由图2可知,点P从A运动到B用了10秒,由行程问题的数量关系可以求出P、Q的运动速度.
(3)作PG⊥y轴于G,BF⊥y轴于F,如图则PG∥BF,△AGP∽△AFB,利用相似三角形对应线段成比例表示出三角形POQ的高,根据三角形的面积公式就可以求出(2)中面积S(平方单位)与时间t(秒)的函数关系式.然后转化为顶点式就可以求出最值了.
(4)当P在AB 上时,若OP=PQ,如图则作PH⊥x轴,有△AGP∽△AFB;当P在 BC上时,若OP=PQ过P作PH⊥x轴,过B作BF⊥y轴于F,交PH于M.有△PBM∽△BAF,有相似三角形的性质就可以求出点P的坐标.
点评:本题考查了相似三角形的判定与性质,勾股定理的运用,三角形的面积的运用,二次函数解析式的运用,坐标与图象的性质及动点问题的解答.

 如图1,等腰直角△ABC的顶点A,B的坐标分别为(0,10),(8,4),顶点C在第一象限.点P从点A出发,沿△ABC的边按逆时针方向匀速运动,同时,点O从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时.P、Q两点同时停止运动,设运动的时间为t秒,
如图1,等腰直角△ABC的顶点A,B的坐标分别为(0,10),(8,4),顶点C在第一象限.点P从点A出发,沿△ABC的边按逆时针方向匀速运动,同时,点O从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时.P、Q两点同时停止运动,设运动的时间为t秒,
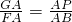 ,
, t,
t, t,
t, OQ×OG=
OQ×OG= (4+t)( 10-
(4+t)( 10- t)
t)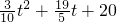
 (t2-
(t2- t)+20
t)+20 (t-
(t- )2+
)2+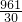
 时,S有最大值,此时,GP=
时,S有最大值,此时,GP=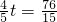 ,OG=10-
,OG=10- t=
t=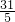
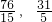 )
)  OQ=
OQ=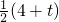 .
.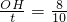 ,OH=
,OH=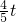
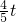 =
=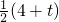 ,t=
,t=
 OQ=
OQ=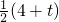 ,PB=t-10,BA=10,AF=6,
,PB=t-10,BA=10,AF=6,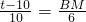 ,BM=
,BM= (t-10),
(t-10), (t-10)=
(t-10)=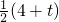 ,t=0(舍去),
,t=0(舍去), 时,OP=PQ
时,OP=PQ


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
