
 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH丄AB于H,交AO于G,连接0H.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH丄AB于H,交AO于G,连接0H.分析 (1)根据菱形的性质得到AC⊥BD,由于DH⊥AB于H,于是得到∠DHA=∠DOG=90°,推出△AGH∽△DGO,根据相似三角形的性质得到$\frac{AG}{DG}=\frac{HG}{OG}$,于是得到结论;
(2)根据已知条件得到∠DAB=60°,AB=AD=6,得到△ABD是等边三角形,根据菱形的性质得到AC⊥DB,OD=OB=$\frac{1}{2}$BD=3,得到∠ODG=30°,解直角三角形即可得到结论.
解答 (1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵DH⊥AB于H,
∴∠DHA=∠DOG=90°,
∵∠AGH=∠DGO,
∴△AGH∽△DGO,
∴$\frac{AG}{DG}=\frac{HG}{OG}$,
∴AG•GO=HG•GD;
(2)解:∵四边形ABCD是菱形,∠ABC=120°,
∴∠DAB=60°,AB=AD=6,
∴△ABD是等边三角形,
∵AC⊥DB,OD=OB=$\frac{1}{2}$BD=3,
∵DH⊥AB,
∴∠ODG=30°,
∴OG=OD•tan30°=$\sqrt{3}$.
点评 本题考查了相似三角形的判定和性质,菱形的性质,直角三角形的性质,熟记个性质定理是解题的关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | -$\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
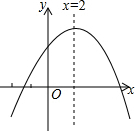 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=2.下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=2.下列结论中正确的是( )| A. | abc>0 | B. | 5a+c>0 | C. | 4a-b=0 | D. | 9a+3b+c<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com