
【题目】已知一次函数y1=﹣2x﹣3与y2=![]() x+2.
x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>![]() x+2的解集为多少?
x+2的解集为多少?
(3)求两图象和y轴围成的三角形的面积.

【答案】(1)l图象见解析;(2)x<﹣2;(3)5.
【解析】试题(1)先求出直线y1=-2x-3,y2=![]() x+2与x轴和y轴的交点,再画出两函数图象即可;
x+2与x轴和y轴的交点,再画出两函数图象即可;
(2)直线y1=-2x-3的图象落在直线y2=![]() x+2上方的部分对应的x的取值范围就是不等式-2x-3>
x+2上方的部分对应的x的取值范围就是不等式-2x-3>![]() x+2的解集;
x+2的解集;
(3)根据三角形的面积公式求解即可.
试题解析:(1)函数y1=﹣2x﹣3与x轴和y轴的交点分别是(﹣1.5,0)和(0,﹣3),
y2=![]() x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),
x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),
其图象如图:

(2)观察图象可知,函数y1=﹣2x﹣3与y2=![]() x+2交于点(﹣2,1),
x+2交于点(﹣2,1),
当x<﹣2时,直线y1=﹣2x﹣3的图象落在直线y2=![]() x+2的上方,即﹣2x﹣3>
x+2的上方,即﹣2x﹣3>![]() x+2,
x+2,
所以不等式﹣2x﹣3>![]() x+2的解集为x<﹣2;
x+2的解集为x<﹣2;
故答案为x<﹣2;
(3)∵y1=﹣2x﹣3与y2=![]() x+2与y轴分别交于点A(0,﹣3),B(0,2),
x+2与y轴分别交于点A(0,﹣3),B(0,2),
∴AB=5,
∵y1=﹣2x﹣3与y2=![]() x+2交于点C(﹣2,1),
x+2交于点C(﹣2,1),
∴△ABC的边AB上的高为2,
∴S△ABC=![]() ×5×2=5.
×5×2=5.


科目:初中数学 来源: 题型:
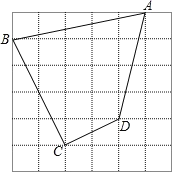
【题目】如图,每个小正方形的边长都为1.四边形ABCD每个顶点分别都在格点上,请按要求完成下列各题:
(1)请在空白图中画出一个三角形,使其周长为![]() ,所画图形中各顶点必须与网格中的小正方形的顶点重合。
,所画图形中各顶点必须与网格中的小正方形的顶点重合。
(2) 求四边形ABCD的面积 。
(3)∠BCD是直角吗 ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地![]() ,如图所示,现计划在空地上种植草皮,经测量
,如图所示,现计划在空地上种植草皮,经测量![]() ,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为![]() 的正方形图形分割成四部分,观察图形,解答下列问题:
的正方形图形分割成四部分,观察图形,解答下列问题:
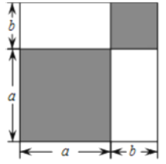
(1)根据图中条件,请用两种方法表示该阴影图形的总面积
方法1:_________________方法2__________________;
由此可得等量关系:______________________________;
应用该等量关系解决下列问题:
(2)若图中的a,b(![]() )满足
)满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
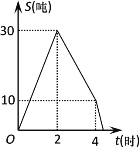
A. 4小时B. 4.4小时C. 4.8小时D. 5小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A.
(1)当x取何值时y1>y2?
(2)当直线BA平分△BOC的面积时,求点A的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com