
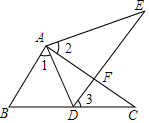
 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,试说明:△ABC≌△ADE的理由.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,试说明:△ABC≌△ADE的理由.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
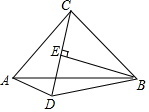 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD,BE⊥CD,垂足分别为点D、点E,连接BD.
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD,BE⊥CD,垂足分别为点D、点E,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
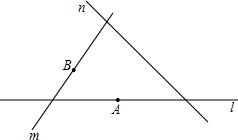 如图,某住宅小区拟在休闲场地的三条道路m,n,l上修建三个凉亭A、B、C且凉亭与长廊两两连通.如果凉亭A、B的位置己经选定,那么凉亭C建在道路l上的什么位置,才能使工程造价最低?请用尺规作出图形(不写作法,但保留作图痕迹)
如图,某住宅小区拟在休闲场地的三条道路m,n,l上修建三个凉亭A、B、C且凉亭与长廊两两连通.如果凉亭A、B的位置己经选定,那么凉亭C建在道路l上的什么位置,才能使工程造价最低?请用尺规作出图形(不写作法,但保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com