
����Ŀ������Ҫ��ش�����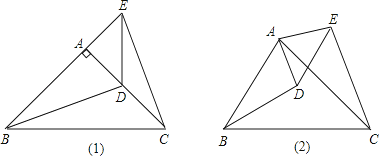
��1����ͼ���ڡ�ABC�͡�ADE�У�AB=AC��AD=AE����BAC=��DAE=90�㣮
�ٵ���D��AC��ʱ����ͼ1���߶�BD��CE��������������ϵ��λ�ù�ϵ��ֱ��д�������Ľ��ۣ�
�ڽ�ͼ1�еġ�ADE�Ƶ�A˳ʱ����ת���ǣ�0�㣼����90�㣩����ͼ2���߶�BD��CE��������������ϵ��λ�ù�ϵ����˵�����ɣ�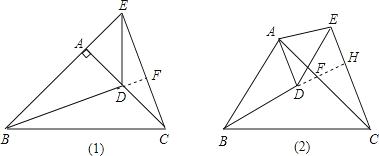
��2������ABC�͡�ADE��������ס��ҡ����е��ĸ�����ʱ��ʹ�߶�BD��CE�ڣ�1���е�λ�ù�ϵ��Ȼ����������˵�����ɣ�
�ף�AB��AC=AD��AE=1����BAC=��DAE��90�㣻
�ң�AB��AC=AD��AE��1����BAC=��DAE=90�㣻
����AB��AC=AD��AE��1����BAC=��DAE��90�㣮
���𰸡�
��1��
�⣺�ٽ��ۣ�BD=CE��BD��CE��
�ڽ��ۣ�BD=CE��BD��CE��1��
�������£��ߡ�BAC=��DAE=90��
���BAC����DAC=��DAE����DAC������BAD=��CAE��1��
�ڡ�ABD���ACE�У�
�� 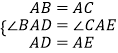
���ABD�ա�ACE��SAS��
��BD=CE
�ӳ�BD��AC��F����CE��H��
�ڡ�ABF���HCF�У�
�ߡ�ABF=��HCF����AFB=��HFC
���CHF=��BAF=90��
��BD��CE
��2��
�⣺���ۣ��ң�AB��AC=AD��AE����BAC=��DAE=90��
����������1����BD=CE��BD��CE������ȫ�������ε��ж�����SAS��֪��ABD�ա�ACE��Ȼ����ȫ�������εĶ�Ӧ�����֤��BD=CE����Ӧ����ȡ�ABF=��ECA��Ȼ���ڡ�ABD�͡�CDF�У����������ڽǺͶ���������á�CFD=90�㣬��BD��CF��
��BD=CE��BD��CE������ȫ�������ε��ж�����SAS��֪��ABD�ա�ACE��Ȼ����ȫ�������εĶ�Ӧ�����֤��BD=CE����Ӧ����ȡ�ABF=��ECA���������ߣ��ӳ�BD��AC��F����CE��H��BH�����Զ��ǡ�ABF=��HCF���ٸ����������ڽǺͶ���֤�á�BHC=90�㣻��2�����ݽ��ۢ١��ڵ�֤������֪����BAC=��DFC�����FHC=90�㣩ʱ���ý��۳����ˣ����Ա������еġ�BAC=��DAE��90�㲻���ʣ�


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
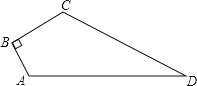
����Ŀ����ͼ����֪�ı���ABCD�У���B=90�㣬AB=3��BC=4��CD=12��AD=13�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��λ����ͼ��ʾ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���
��1������ABC��x�᷽������ƽ��6����λ������ƽ�ƺ�õ��ġ�A1B1C1��
��2������ABC���ŵ�A˳ʱ����ת90�㣬������ת��õ��ġ�AB2C2����ֱ��д����B2��C2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������Ϊ4�ĵ���ֱ�������η���ֱ������ϵ�У�˳�����Ӹ����е�õ���1�������Σ���˳�����Ӹ����е�õ���2����������������˲�����ȥ����ô����6�������ε�ֱ�Ƕ�������Ϊ��������

A. ����![]() ��
��![]() �� B. ����
�� B. ����![]() ��
��![]() �� C. ����
�� C. ����![]() ��
��![]() �� D. ����
�� D. ����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���E��F�ڶԽ���BD�ϣ���BE=DF����֤��
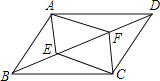
��1����ABE�ա�CDF��
��2���ı���AECF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У������ȷ���ǣ� ��
A.����2y��3=��6y3
B.����ab2��3=��ab6
C.����a��3�£���a2��=a
D.�� ![]() ����1��22=2
����1��22=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
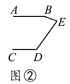
����Ŀ����һ����С��ͬѧ�������λ�������ͼ�����Ȼ�������ƽ����AB��CD��Ȼ����ƽ���仭��һ��E������BE��DE����ͼ������������������ס��E���϶��ֱ�õ���ͼ������������ͼ�Σ���ʱ��ͻȻһ�룬��B����D���BED֮��Ķ�����û��ij����ϵ�أ�����С��ͬѧͨ�����������λ��������������Ƕ����������������ܣ��ҵ�����������֮��Ĺ�ϵ��
��1������̽����ͼ����ͼ����ͼ�еġ�B����D���BED֮��Ĺ�ϵ��
��2�����ͼ�ڢۢ��У�ѡһ��˵�������������ɣ�
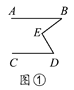
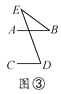
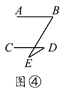
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
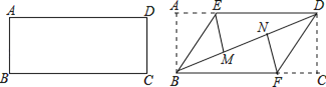
����Ŀ����һ�ž���ֽƬ������ͼ����������ABE��BE���ۣ�ʹ��A���ڶԽ���BD�ϵ�M�㣬����CDF��DF���ۣ�ʹ��C���ڶԽ���BD�ϵ�N�㣮
��1����֤���ı���BFDE��ƽ���ı���.
��2�����ı���BFDE�����Σ�BE =2��������BFDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2��2ax+c��y�ύ��C�㣬��x�ύ��A��B���㣬��A�������ǣ���1��0����O������ԭ�㣬��|OC|=3|OA|
��1���������ߵĺ�������ʽ��
��2��ֱ��д��ֱ��BC�ĺ�������ʽ��
��3����ͼ1��DΪy��ĸ������ϵ�һ�㣬��OD=2����ODΪ����������ODEF����������ODEF��ÿ��1����λ���ٶ���x����������ƶ������˶������У���������ODEF���OBC�ص����ֵ����Ϊs���˶���ʱ��Ϊt�루0��t��2����
��s��t֮��ĺ�����ϵʽ��
�����˶������У�s�Ƿ�������ֵ��������ڣ�ֱ��д��������ֵ����������ڣ���˵�����ɣ�
��4����ͼ2����P��1��k����ֱ��BC�ϣ���M��x���ϣ���N���������ϣ��Ƿ������A��M��N��PΪ�����ƽ���ı��Σ������ڣ���ֱ��д��M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com