
 如图,AB,CD是圆O的直径,且AB⊥CD,P为CD延长线上一点,PE切圆O于E,BE交CD于F,AB=6cm,PE=4cm,则EF的长为$\frac{4\sqrt{10}}{5}$cm.
如图,AB,CD是圆O的直径,且AB⊥CD,P为CD延长线上一点,PE切圆O于E,BE交CD于F,AB=6cm,PE=4cm,则EF的长为$\frac{4\sqrt{10}}{5}$cm. 分析 连接OE,可求得∠PEF=∠PFE,可求得PF,在Rt△OBF中由勾股定理可求得BF,再利用相交弦定理可求得EF的长.
解答 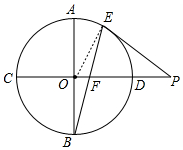 解:
解:
如图,连接OE,
∵∠PEF=90°-∠OEB=90°-∠OBE=∠OFB=∠EFP,
∴PF=PE=4,
在Rt△OPE中,由勾股定理可得OP2=PE2+OE2,
∴OP2=32+42=25,解得OP=5cm,
∴OF=OP-PF=5-4=1(cm),DF=OD-OF=2cm,CF=OF+OC=4cm,
在Rt△OBF中,由勾定理可得BF2=OB2+OF2,
即BF2=32+12=10,
∴FB=$\sqrt{10}$cm,
又由相交弦定理可知BF•EF=CF•DF,
∴EF=$\frac{4×2}{\sqrt{10}}$=$\frac{4\sqrt{10}}{5}$cm,
故答案为:$\frac{4\sqrt{10}}{5}$.
点评 本题主要考查切线的性质及垂径定理,证得PE=PF是解题的关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,已知直线l1:y=3x+1和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
如图,已知直线l1:y=3x+1和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com