
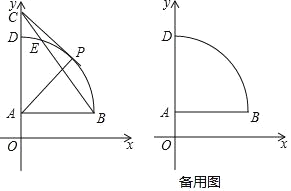
����Ŀ����ͼ��A(0��2)��B(6��2)��C(0��c)(c��0)����AΪԲ��AB��Ϊ�뾶��![]() ��y���������ڵ�D��
��y���������ڵ�D��![]() ��BC�н���ʱ������ΪE��PΪ
��BC�н���ʱ������ΪE��PΪ![]() ��һ�㣮
��һ�㣮
(1)��c��6![]() +2��
+2��
��BC��_____��![]() �ij�Ϊ_____��
�ij�Ϊ_____��
�ڵ�CP��6![]() ʱ���ж�CP���A��λ�ù�ϵ��������֤����
ʱ���ж�CP���A��λ�ù�ϵ��������֤����
(2)��c��10�����P��BC��������ֵ��
(3)�ֱ�ֱ��д����c��1��c��6��c��9��c��11ʱ����P��BC��������(������軯��)
���𰸡�(1)��12��������CP���A���У�(2)��c��10����P��BC��������ֵ��![]() ��(3)c=1ʱ��PM=
��(3)c=1ʱ��PM=![]() ��c=6ʱ��PF��6��
��c=6ʱ��PF��6��![]() ��c=9ʱ��PF��6��
��c=9ʱ��PF��6��![]() ��c=11ʱ��PG��
��c=11ʱ��PG��![]() .
.
��������
(1)�������AB��AC���������BC�͡�ABC������û�����ʽ���ɵó����ۣ����жϳ���APC��ֱ�������Σ����ɵó����ۣ�
(2)��������������������ε������������Ǻ������ɵó����ۣ�
(3)��ͼͼ�Σ�ͬ(2)�ķ������ɵó����ۣ�
�⣺(1)����ͼ1������AE��
��c��6![]() +2��
+2��
��OC��6![]() +2��
+2��
��AC��6![]() +2��2��6
+2��2��6![]() ����AB��6��
����AB��6��
��Rt��BAC�У����ݹ��ɶ����ã�BC��12��tan��ABC��![]() ��
��![]() ��
��
���ABC��60����
��AE��AB��
���ABE�ǵȱ������Σ�
���BAE��60����
���DAE��30����
��![]() �ij�Ϊ
�ij�Ϊ![]() ������
������
�ʴ�Ϊ12������

��CP���A����
֤������AP��AB��6��AC��OC��OA��6![]() ��
��
��AP2+CP2��108��
��AC2��(6![]() )2��108��
)2��108��
��AP2+PC2��AC2��
���APC��90��������CP��AP��
��AP�ǰ뾶��
��CP���A����
(2)��c��10����AC��10��2��8����BC��10��
������P��![]() �ϣ�AP��BEʱ����P��BC�ľ�������费��ΪF��
�ϣ�AP��BEʱ����P��BC�ľ�������费��ΪF��
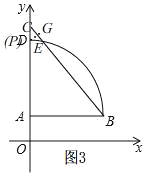
��PF�ij����������룬��ͼ2��
S��ABC��![]() AB��AC��
AB��AC��![]() BC��AF��
BC��AF��
��AF��![]() ��
��![]() ��
��
��PF��AP��AF��![]()

����ͼ3������P��![]() �ϣ���PG��BC�ڵ�G��
�ϣ���PG��BC�ڵ�G��
����P���D�غ�ʱ��PG���
��ʱ��sin��ACB��![]() ��
��
��PG��![]() ��
��![]() ��
��
����c��10����P��BC��������ֵ��![]() ��
��
(3)��c��1ʱ����ͼ4

����P��PM��BC��sin��BCP��![]()
��PM��![]() ��
��![]() ��
��
��c��6ʱ����ͼ5��ͬc��10�Ģ������PF��6��![]() ��
��

��c��9ʱ����ͼ6��ͬc��10�Ģ������PF��6��![]() ��
��

��c��11ʱ����ͼ7��

��P�͵�D�غ�ʱ����P��BC�ľ������ͬc��10ʱ�������PG��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ij����5000����Ϊ�˹��Ƹ������и���������������������в�����3�Σ�ȡ�õ��������£�
����/�� | ƽ��ÿ���������/kg | |
��1��� | 20 | 1.6 |
��2��� | 15 | 2.0 |
��3��� | 15 | 1.8 |
��1����������ƽ��ÿ�����������
��2������������������������
��3���������ÿǧ�˵��ۼ�Ϊ14Ԫ������۸����������y��Ԫ������۸����������x��kg��֮��ĺ�����ϵ���������Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
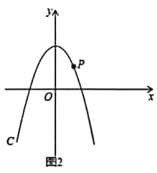
����Ŀ����ͼ1����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��![]() ���ཻ��
���ཻ��![]() ���㣬����Ϊ
���㣬����Ϊ![]() �����
�����![]() ��
��![]() �����������һ�㣬��������
�����������һ�㣬��������![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() ���õ��µ�������
���õ��µ�������![]() ��
��

![]() ��������
��������![]() �ĺ�������ʽ:
�ĺ�������ʽ:
![]() ��������
��������![]() ��������
��������![]() ��
��![]() ����Ҳ���������ͬ�Ĺ����㣬��
����Ҳ���������ͬ�Ĺ����㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ��ͼ2��
��ͼ2��![]() �ǵ�һ������������
�ǵ�һ������������![]() ��һ�㣬������������ľ�����ȣ���
��һ�㣬������������ľ�����ȣ���![]() ��������
��������![]() �ϵĶ�Ӧ��
�ϵĶ�Ӧ��![]() ����
����![]() ��
��![]() �ϵĶ��㣬
�ϵĶ��㣬![]() ��
��![]() �ϵĶ��㣬��̽���ı���
�ϵĶ��㣬��̽���ı���![]() �ܷ��Ϊ�����Σ����ܣ����
�ܷ��Ϊ�����Σ����ܣ����![]() ��ֵ�������ܣ���˵�����ɣ�
��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����BD�ǡ�O���ң��ӳ�BD����C��ʹDC��BD������AC��EΪAC��һ�㣬ֱ��ED��AB�ӳ��߽��ڵ�F������CDE����DAC��AC��12��

��1�����O�뾶��
��2����֤��DEΪ��O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
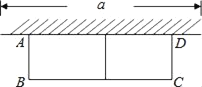
����Ŀ����ͼ���г�Ϊ 24m ����ʣ���һ������ǽ��ǽ�������ó��� a Ϊ 10m��Χ���м����һ����ʵij����λ��ԣ��軨�ԵĿ� AB Ϊ xm�����Ϊ Sm2��
��1�� �� S �� x �ĺ�����ϵʽ�� x ֵ��ȡֵ��Χ��
��2�� ҪΧ�����Ϊ 45m2 �Ļ��ԣ�AB �ij��Ƕ����ף�
��3�� �� AB �ij��Ƕ�����ʱ��Χ�ɵĻ��Ե�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�ڣ���ԭ��OΪԲ�ģ�1Ϊ�뾶��Բ����P��ֱ��![]() ���˶�������P����Բ��һ�����ߣ��е�ΪA����PA����СֵΪ
���˶�������P����Բ��һ�����ߣ��е�ΪA����PA����СֵΪ![]() ����
����![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��Ϊ������ȫ�������������ƺţ���ĩ����ί��֯־Ը�߽��������.����������ʦ������4��Ů��ɲ���С�á�С�ݡ�С��Сٻ����ͨ����ǩ�ķ�ʽȷ��2��Ů��ȥ�μ�.
��ǩ����4��Ů��ɲ������ֱ�д��4����ȫ��ͬ�Ŀ�Ƭ���棬�����ſ�Ƭ���泯�ϣ�ϴ�Ⱥ���������ϣ�����ʦ�ȴ��������ȡһ�ſ�Ƭ�������������ٴ�ʣ���3�ſ�Ƭ�������ȡ�ڶ��ţ���������.
��1���ð�������С�ձ��������� �¼�����С�ñ��������� �¼�(������������������Ȼ�����������)����һ�γ�ȡ��Ƭ��С�ñ��������ĸ���Ϊ ��
��2�����û���״ͼ���б��ķ�����ʾ��γ�ǩ���п��ܵĽ�����������С�ݱ��������ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���![]() ����
����![]() ������
������![]() ��ֱ��
��ֱ��![]() ��ֱ���߶�
��ֱ���߶�![]() ����
����![]() ��ֱ��
��ֱ��![]() ���ڵ�һ�����ڵ�һ���㣬����
���ڵ�һ�����ڵ�һ���㣬����![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ����
����![]() ��
��![]() ����
����![]() ��ʹ��
��ʹ��![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ��
��![]() ��
��![]() Ϊ��������������ABP���ƣ�������������ĵ�
Ϊ��������������ABP���ƣ�������������ĵ�![]() ������Ϊ__________��
������Ϊ__________��
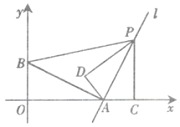
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB��BC��
��1�����ó߹���ͼ����AD����ȷ����E��ʹ��E����AB��BC�ľ�����ȣ���д������������ͼ�ۼ�����
��2����BC=8��CD=5����DE= ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com