

分析 (1)i.根据轴对称的性质,可求得相等的线段与角,可得点M是AB中点,即当x=$\frac{1}{2}$AB=2时,点P恰好落在边BC上;
ii.分两种情况讨论:①当0<x≤2时,△MNP与梯形BCNM重合的面积为△MNP的面积,根据轴对称的性质△MNP的面积等于△AMN的面积,易见y=$\frac{3}{8}$x2
②当2<x<4时,如图2,设PM,PN分别交BC于E,F,由i.知ME=MB=4-x∴PE=PM-ME=x-(4-x)=2x-4,由题意知△PEF∽△ABC,利用相似三角形的性质即可求得.
(2)利用分类讨论的思想,先求的直线BC与⊙O相切时,x的值,然后得到相交,相离时x的取值范围.
解答 解:(1)i.如图1,由轴对称性质知:AM=PM,∠AMN=∠PMN,
又MN∥BC,
∴∠PMN=∠BPM,∠AMN=∠B,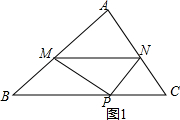
∴∠B=∠BPM,
∴AM=PM=BM,
∴点M是AB中点,即当x=$\frac{1}{2}$AB=2时,点P恰好落在边BC上.
ii.以下分两种情况讨论:
①当0<x≤2时,
∵MN∥BC,
∴△AMN∽△ABC,
∴$\frac{AM}{AB}=\frac{AN}{AC}$,
∴$\frac{x}{4}=\frac{AN}{3}$,
∴AN=$\frac{3}{4}x$,
△MNP与梯形BCNM重合的面积为△MNP的面积,
∴y=$\frac{1}{2}$•$\frac{3x}{4}$•x=$\frac{3}{8}$x2
y=$\frac{{3x}^{2}}{8}$,
②当2<x<4时,如图2,设PM,PN分别交BC于E,F,
由(2)知ME=MB=4-x,
∴PE=PM-ME=x-(4-x)=2x-4,
由题意知△PEF∽△ABC,
∴${(\frac{PE}{AB})}^{2}$=$\frac{{S}_{△PEF}}{{S}_{△ABC}}$,
∴S△PEF=$\frac{3}{2}$(x-2)2,
∴y=S△PMN-S△PEF=$\frac{3}{8}$x2-${\frac{3}{2}(x-2)}^{2}$=$-\frac{9}{8}$x2+6x-6,
∴y=$\left\{\begin{array}{l}{\frac{3}{8}{x}^{2}(0<x≤2)}\\{-\frac{9}{8}{x}^{2}+6x-6(2<x<4)}\end{array}\right.$,
∵当0<x≤2时,y=$\frac{3}{8}$x2,
∴易知y最大=${\frac{3}{8}×2}^{2}$=$\frac{3}{2}$,
又∵当2<x<4时,y=-$\frac{9}{8}$x2+6x-6=$-\frac{9}{8}$(x-$\frac{8}{3}$)2+2,
∴当x=$\frac{8}{3}$时(符合2<x<4),y最大=2,
综上所述,当x=$\frac{8}{3}$时,重叠部分的面积最大,其值为2.
(2))如图3,设直线BC与⊙O相切于点D,连接AO,OD,则AO=OD=$\frac{1}{2}$MN.
在Rt△ABC中,BC=$\sqrt{{AB}^{2}{+AC}^{2}}$=5;
由(1)知△AMN∽△ABC,
∴$\frac{AM}{AB}=\frac{MN}{BC}$,即$\frac{x}{4}=\frac{MN}{5}$,
∴MN=$\frac{5}{4}$x
∴OD=$\frac{5}{8}$x,
过M点作MQ⊥BC于Q,则MQ=OD=$\frac{5}{8}$x,
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴$\frac{BM}{BC}=\frac{QM}{AC}$,
∴BM=$\frac{BC•QM}{AC}$=$\frac{25}{24}$x,AB=BM+MA=$\frac{25}{24}$x+x=4
∴x=$\frac{96}{49}$,
∴当x=$\frac{96}{49}$时,⊙O与直线BC相切;
当x<$\frac{96}{49}$时,⊙O与直线BC相离;
x>$\frac{96}{49}$时,⊙O与直线BC相交.
点评 本题主要考查了折叠问题,相似三角形的性质,注意对应的线段对应的角相等,数形结合思想的应用,分类讨论是解答此题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.
如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-$\sqrt{2}$x=5 | B. | x(3x-5)-6=0 | C. | x2-x+1=0 | D. | x2-6x+9=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
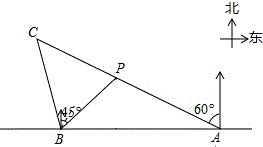 如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com