
当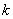 满足条件
满足条件 时,关于
时,关于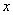 的一元二次方程
的一元二次方程 是否存在实数根
是否存在实数根 ,若存在求出
,若存在求出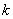 值,若不存在请说明理由.
值,若不存在请说明理由.
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
如图,抛物线y= a(x﹣1)2+c与x轴交于点A(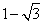 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)图中是否存在与△ODM相似的三角形,若存在,请找出并给于证明。
(2)设DM = x,OA=R,求R关于x 的函数关系式;是否存在整数R,使得正方形ABCD内部的扇形OAM围成的圆锥地面周长为 p ,若存在请求出此时DM的长;不存在,请说明理由。
p ,若存在请求出此时DM的长;不存在,请说明理由。
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将矩形ABCD沿对角线BD折叠,使C落在C′处,BC′交AD于点E,则下到结论不一定成立的是 ( )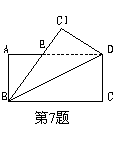
A、AD=BC′ B、∠EBD=∠EDB
C、△ABE∽△CBD D、Cos∠AEB =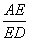
查看答案和解析>>
科目:初中数学 来源: 题型:
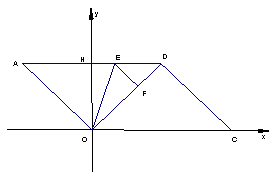
如图,在直角坐标系中,平行四边形AOCD的边OC在x轴上,边AD与y轴交与点H,CD=10,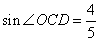 。点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),
。点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),
∠OEF=∠A=∠DOC,设AE=t,OF=s。
(1) 求直线DC的解析式;
(2) 求s关于t的函数关系式,并写出t的取值范围;
(3) 点E在边AD上移动的过程中,△OEF是否有可能成为一个等腰三角形?若有可能,请求出t的值,若不可能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com