
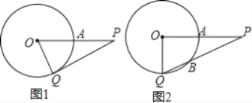
【题目】已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
【答案】(1) ∠QOP=60°; (2) QB=![]() .
.
【解析】
(1)先利用切线的性质得到OQ⊥PQ,然后利用锐角三角函数值的定义求∠QOP的大小;
(2)利用垂径定理,作OD⊥BQ于D,如图2,则QD=BD,先利用勾股定理计算出PQ,再证明Rt△QOD∽Rt△QPO,利用相似比计算出QD,从而得到BQ的长.
(1)如图1,∵PQ是⊙O的切线,∴OQ⊥PQ,∵A是OP的中点,∴OP=2OA,
在Rt△OPQ中,cos∠QOP=![]() =
=![]() ,∴∠QOP=60°;
,∴∠QOP=60°;
(2)作OD⊥BQ于D,如图2,则QD=BD,∵∠QOP=90°,OP=4,OQ=2,∴PQ=2![]() ,
,
∵∠OQD=∠PQO,∴Rt△QOD∽Rt△QPO,∴QD:OQ=OQ:QP,即QD:2=2:2![]() ,
,
∴QD=![]() ,∴QB=2QD=
,∴QB=2QD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在一条直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
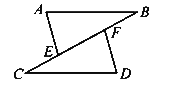
(1)求证:AB=CD;
(2)若AB=CF,∠B=50°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )

A.AB=CDB.AB∥CDC.∠A=∠CD.BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
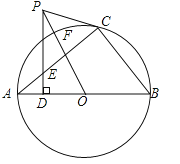
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
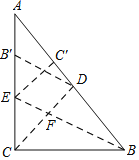
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B′处,展开后,再沿BE折叠,使点C落在BA边上的C′处,CD与BE交于点F.
(1)求AC′的长度;
(2)求CE的长度;
(3)比较四边形EC′DF与△BCF面积的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
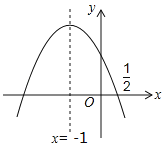
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com