
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
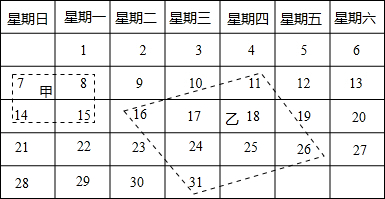
如图是2003年12月份的日历牌,我们在日历牌中用两种不同的方式选择四个数。
(1)从甲种选择构成的“矩形”中发现14×8-7×15=7,即对角线上两数积的差为7。请你平移矩形甲,使它的四个顶点落在其他的四个数上,对角线上的两数积的差还为7吗?
(2)对乙种选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,你又能得出什么结论?
(3)由第(1)、(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请假设所选择的某个数为n,然后通过含n的代数式的运算加以说明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com