练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示的一块地，已知∠ADC=90°，AD=12m，CD=9m，AB=25m，BC=20m，则这块地的面积为（　　）平方米．

    A. 96 B. 204 C. 196 D. 304

    A 【解析】连接AC，运用勾股定理逆定理可证△ACD，△ABC为直角三角形，可求出两直角三角形的面积，此块地的面积为两个直角三角形的面积差． 【解析】 连接AC， 则在Rt△ADC中， AC2=CD2+AD2=122+92=225， ∴AC=15，在△ABC中，AB2=1521， AC2+BC2=152+362=1521， ∴AB2=AC2+BC2， ∴∠ACB=90...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    若一元二次方程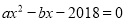有一根为，则__________．

    2018 【解析】试题解析: 把x=?1代入方程有： a+b?2018=0， 即a+b=2018. 故答案为:2018.

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：填空题

    关于x的一元二次方程x2＋2x－2m＋1=0的两实数根之积为负，则实数m的取值范围是______________

    m>0.5 【解析】试题解析：关于的一元二次方程的两实数根之积为负， 解得： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：解答题

    计算：|﹣2|+﹣（﹣1）2017．

    1 【解析】试题分析：根据绝对值，立方根和-1的奇数次幂的计算法则求出各数的值，然后进行求和得出答案． 试题解析：原式=2﹣2+1=1．

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：填空题

    计算：（﹣）﹣2+（﹣2017）0=_____．

    5 【解析】原式=4+1=5.

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：单选题

    式子在实数范围内有意义，则x的取值范围是（）

    A. x＞1 B. x≥1 C. x＜1 D. x≤1

    B 【解析】试题分析：根据被开方数大于等于0列式计算即可得解．由题意得，x﹣1≥0， 解得x≥1．故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：解答题

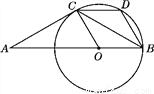
    如图，△ABC是等腰三角形，且AC＝BC，∠ACB＝120°，在AB上取一点O，使OB＝OC，以点O为圆心，OB为半径作圆，过点C作CD∥AB交⊙O于点D，连接BD.

    (1)猜想AC与⊙O的位置关系，并证明你的猜想；

    (2)试判断四边形BOCD的形状，并证明你的判断；

    (3)已知AC＝6，求扇形OBC所围成的圆锥的底面圆的半径r.

    (1)猜想：AC与⊙O相切(2)四边形BOCD为菱形(3) 【解析】试题分析：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了菱形的判定方法和圆锥的计算．（1）根据等腰三角形的性质得∠A=∠ABC=30°，再由OB=OC得∠OCB=∠OBC=30°，所以∠ACO=∠ACB-∠OCB=90°，然后根据切线的判定定理即可得到，AC是⊙O的切线； （2）连结...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为，则可列方程为（  ）。

    A. 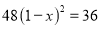B.

    C. D.

    D 【解析】试题分析：依题意得三月份的营业额为36(1＋x)2， ∴36(1＋x)2＝48． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：单选题

    如图，小叶与小高欲测量公园内某棵树DE的高度．他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m，台阶AC的坡度为1∶，且B，C，E三点在同一条直线上，那么这棵树DE的高度为(　　)

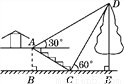
    A. 6 m B. 7 m C. 8 m D. 9 m

    D 【解析】过点A作AF⊥DE于点F，则四边形ABEF为矩形， ∴AF＝BE，EF＝AB＝3m． 设DE＝xm，在Rt△CDE中，CE＝＝xm． 在Rt△ABC中，∵＝，AB＝3m， ∴BC＝3m． 在Rt△AFD中，DF＝DE－EF＝(x－3) m， ∴AF＝＝ (x－3) m． ∵AF＝BE＝BC＋CE， ∴ (x－3)＝3＋x， 解...

    查看答案和解析>>

    同步练习册答案