
【题目】如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.

【答案】因为∠l=∠2(已知)
∠2=∠3(对顶角相等)
所以∠l=∠3(等量代换)………………………………………………………2分
所以BD∥CE(同位角相等,两直线平行)……………………………………4分
所以∠C=∠DBA(两直线平行,同位角相等)………………………………6分
又因为∠C=∠D(已知)
所以∠DBA=∠D(等量代换)…………………………………………………8分
所以DF∥AC(内错角相等,两直线平行)………………………………………9分
所以∠A=∠F(两直线平行,内错角相等)…………………………………………10分
【解析】
试题根据对顶角的性质得到BD∥CE的条件,然后根据平行线的性质得到∠B=∠C,已知∠C=∠D,则得到满足AB∥EF的条件,再根据两直线平行,内错角相等得到∠A=∠F.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.


科目:初中数学 来源: 题型:
【题目】阅读后回答问题:
计算(-![]() )÷(-15)×(-
)÷(-15)×(-![]() )
)
解:原式=-![]() ÷[(-15)×(-
÷[(-15)×(-![]() )] ①
)] ①
=-![]() ÷1 ②
÷1 ②
=-![]() ③
③
()上述的解法是否正确?答:_________________________
若有错误,在哪一步?答:_________________________(填代号)
错误的原因是:___________________________________
(2)这个计算题的正确答案应该是:______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图平面直角坐标系内,已知点A的坐标是(-3,0).
(1)点B的坐标为_______,点C的坐标为_____,∠BAC=______;
(2)求△ABC的面积;
(3)点P是y轴负半轴上的一个动点,连接BP交![]() 轴于点D,是否存在点P使得
轴于点D,是否存在点P使得
△ADP与△BC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.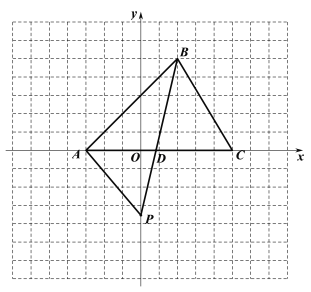
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读求绝对值不等式![]() 和
和![]() 的解集过程:
的解集过程:
对于绝对值不等式![]() ,从图1所示的数轴上看:大于
,从图1所示的数轴上看:大于![]() 而小于
而小于![]() 的数绝对值是小于
的数绝对值是小于![]() 的,所以
的,所以![]() 的解集是
的解集是![]() ;
;
对于绝对值不等式![]() ,从图2所示的数轴上看:小于
,从图2所示的数轴上看:小于![]() 而大于
而大于![]() 的数绝对值是大于
的数绝对值是大于![]() 的,所以
的,所以![]() 的解集…….
的解集…….


解答下面的问题:
解不等式:⑴.![]() ; ⑵.
; ⑵.![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
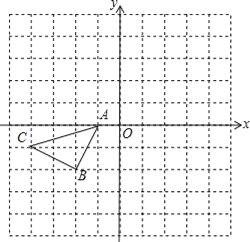
【题目】如图的正方形格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△AB1C1.若△ABC内有一点P(a,b),则经过两次变换后点P的坐标变为 .
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)若将△ABC绕某点逆时针旋转90°后,其对应点分别为A3(2,1),B3(4,0),C3(3,﹣2),则旋转中心坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
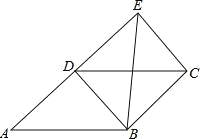
A.AB=BE B.BE⊥DC C.∠ADB=90° D.CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,
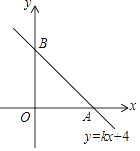
(1)求这条直线的解析式;
(2)若将这条直线沿x轴翻折,求翻折后得到的直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.

(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
(2)用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数;
(3)求第n行各数之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com