
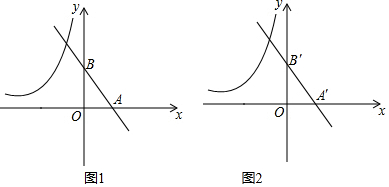
分析 (1)先求AB=BC,作辅助线,得OE=OA=2,即C的横坐标为-2,代入直线AB的解析式可得C的坐标,因为点C在反比例函数的图象上,可得k的值,从而得:双曲线的解析式为y=$\frac{-16}{x}$;
(2)如图2,作辅助线,构建梯形,设设P(x,-$\frac{16}{x}$),利用面积差得S△PBC=4,列关于x的方程,解出即可;
(3)先画出图形,设B'(0,2b),表示M的坐标,根据腰长相等:B'M=A'N,列方程可得b的值,分四种情况讨论可得MN的解析式.
解答 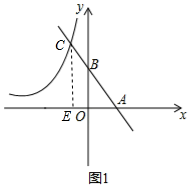 解:(1)如图1,由y=-2x+4得,A(2,0),B(0,4),
解:(1)如图1,由y=-2x+4得,A(2,0),B(0,4),
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=2$\sqrt{5}$,
∴AB=BC,
过C作CE⊥x轴于E,则BO∥CE,
∴OE=OA=2,
把x=-2代入y=-2x+4,得y=8,
∴C(-2,8),
∵C在双曲线y=$\frac{k}{x}$上,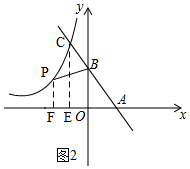
∴k=(-2)×8=-16,
∴双曲线的解析式为y=$\frac{-16}{x}$;
(2)如图2,设P(x,-$\frac{16}{x}$),
∵P在C点左侧,
∴x<-2,
过P作PF⊥x轴于F,过C作CE⊥x轴于E,
∴S△PBC=S梯形PFEC+S梯形CEOB-S梯形PFOB,
=$\frac{1}{2}$(-$\frac{16}{x}$+8)(-x-2)+$\frac{1}{2}$(4+8)×2-$\frac{1}{2}$(-$\frac{16}{x}$+4)•(-x)=4,
4x2=32,
x=$±2\sqrt{2}$,
∵x<-2,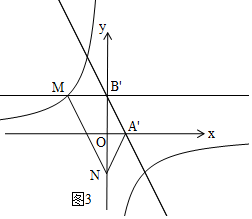
∴x=-2$\sqrt{2}$,
∴P(-2$\sqrt{2}$,4$\sqrt{2}$);
(3)如图3,设B'(0,2b),
∵B′M∥x轴,
∴M(-$\frac{8}{b}$,2b),
∴B′M=$\frac{8}{b}$,
∵AB∥A′B′∥MN,
∴tan∠OB′A′=tan∠MNB′=$\frac{OA′}{OB′}$=$\frac{MB′}{B′N}$=$\frac{1}{2}$,
∴B'N=2B'M=$\frac{16}{b}$,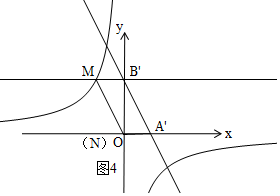
∴ON=B'N-OB'=$\frac{16}{b}$-2b,
∵四边形A′NMB′为等腰梯形,
∴B′M=A′N,
∴$\frac{8}{b}$=$\sqrt{{b}^{2}+(\frac{16}{b}-2b)^{2}}$,
5b4-64b2+192=0,
(b2-8)(5b2-24)=0,
b1=$±2\sqrt{2}$,b2=$±\frac{2\sqrt{30}}{5}$,
设MN的解析式为:y=-2x+k,
①当b=2$\sqrt{2}$时,M(-2$\sqrt{2}$,4$\sqrt{2}$),代入MN的解析式中,得k=0,
∴MN的解析式为:y=-2x,
此时N与O重合,四边形A'NMB'是平行四边形,不符合题意;
②当b=-2$\sqrt{2}$时,M(2$\sqrt{2}$,-4$\sqrt{2}$),代入MN的解析式中,得k=0,
∴MN的解析式为:y=-2x,
四边形A'NMB'是平行四边形,不符合题意;
③当b=$\frac{2\sqrt{30}}{5}$时,M(-$\frac{2\sqrt{30}}{3}$,$\frac{4\sqrt{30}}{5}$),代入MN的解析式中,得k=-$\frac{8\sqrt{30}}{15}$,
∴MN的解析式为:y=-2x-$\frac{8\sqrt{30}}{15}$,
④当b=-$\frac{2\sqrt{30}}{5}$时,M($\frac{2\sqrt{30}}{3}$,-$\frac{4\sqrt{30}}{5}$),代入MN的解析式中,得k=$\frac{8\sqrt{30}}{15}$,
∴MN的解析式为:y=-2x+$\frac{8\sqrt{30}}{15}$,
综上所述,MN的解析式为:y=-2x-$\frac{8\sqrt{30}}{15}$或y=-2x+$\frac{8\sqrt{30}}{15}$.
点评 本题考查了待定系数法、直线与坐标轴的交点、函数图象上点的特征、等腰梯形和平行四边形的性质和判定、三角形和梯形的面积等知识,第3问有难度,计算量大,注意点M在反比例函数的图象上,若四边形A′NMB′为等腰梯形时,当腰B′M=A′N时,B′M与A′N不平行.


科目:初中数学 来源: 题型:选择题
| A. | 当a=-6时,-a的相反数是+6 | |
| B. | 如果a,b都是有理数且|a|>|b|,那么a>b | |
| C. | 如果|a-2|+(1+b)2=0,那么ba=1 | |
| D. | 如果a、b互为相反数,c、d互为倒数,那么$\frac{a+b}{2}$-cd=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
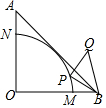 如图,等腰Rt△AOB中,∠AOB=90°,OA=$\sqrt{6}$,⊙O与AB相切,分别交OA、OB于N、M,以PB为直角边作等腰Rt△BPQ,点P在弧MN上由点M运动到点N,则点Q运动的路径长为( )
如图,等腰Rt△AOB中,∠AOB=90°,OA=$\sqrt{6}$,⊙O与AB相切,分别交OA、OB于N、M,以PB为直角边作等腰Rt△BPQ,点P在弧MN上由点M运动到点N,则点Q运动的路径长为( )| A. | $\frac{{\sqrt{3}}}{2}π$ | B. | $\frac{{\sqrt{6}}}{3}π$ | C. | $\sqrt{3}π$ | D. | $\frac{{\sqrt{6}}}{2}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
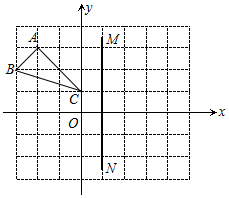 已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点ABC都在格点上,直线MN经过点(1,0)且垂直于x轴,若△A1B1C1和△ABC关于直线MN成轴对称
已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点ABC都在格点上,直线MN经过点(1,0)且垂直于x轴,若△A1B1C1和△ABC关于直线MN成轴对称查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| n | 0.008 | 8 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 0.2 | 2 | 20 | 200 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com