
| 所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 弹簧的长度/cm | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
分析 (1)因为弹簧的长度随所挂物体的质量变化而变化,由此可得结论;
(2)得到所挂物体的质量是0时弹簧的长度即可求解;
(3)由表格中的数据可知,弹簧的长度随所挂物体的重量的增加而增加;
(4)由表中的数据可知,x=0时,y=12,并且每增加1千克的重量,长度增加0.5cm,所以y=0.5x+12;
(5)由(4)中的关系式代入计算即可.
解答 解:(1)上表反映了:弹簧的长度(cm)与所挂物体的质量(kg)之间的关系,物体的质量是自变量,弹簧的长度是自变量的函数;
(2)由表格得:当物体的质量为3kg时,弹簧的长度是9.5cm;
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长;
(4)y与x的关系式为:y=0.5x+12;
(5)当x=14时,y=0.5×14+12=19.
答:当挂重为14千克时,弹簧的长度19cm.
故答案为:物体的质量,弹簧的长度;12cm;增长;y=0.5x+12.
点评 此题主要考查了函数定义、函数关系式以及函数值求法,得出正确的函数关系式是解题关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC,
如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
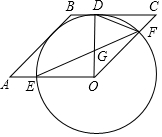 已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.
已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com