
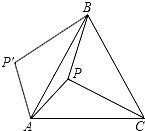
 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$. 分析 连接PP',易证△APP′为等边三角形,同时△PP'B是直角三角形;过点A作AD垂直BP于点D,算出AD、PD,再用勾股定理算出AB,然后用公式直接求出面积.
解答 解:连接PP′,过点A作AD⊥BP于点D,如图,
由旋转性质可知,△APC≌△AP'B,
∴AP=AP',P'B=PC=10,
∵∠P'AP=60°,
∴△APP'是等边三角形,
∴PP'=AP=6,
∵PB=8,
∴P'B2=PB2+P'P2,
∴△PP'B是直角三角形,
∴∠P'PB=90°,
∵∠P'PA=60°,
∴∠APB=150°,
∴∠APD=30°,
∴AD=$\frac{1}{2}AP$=3,PD=$3\sqrt{3}$,
∴BD=8+3$\sqrt{3}$,
在Rt△ABD中,AB2=AD2+BD2=100+48$\sqrt{3}$,
∴${S}_{△ABC}=\frac{\sqrt{3}}{4}A{B}^{2}$=36+25$\sqrt{3}$.
故答案为:150°;36+25$\sqrt{3}$.
点评 本题主要考查了旋转变换的性质、勾股定理及其逆定理、特殊角的三角函数、解直角三角形、等边三角形判定与性质、等边三角形的面积公式等知识点,难度较大.通过旋转的性质得出△APP′为等边三角形以及△PP'B是直角三角形是解答本题的第一个关键;在得出∠APB为150°之后,“将特殊角或其补角放入直角三角形当中”是解答本题的第二个关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}(\overline{a}+\overline{b})$ | B. | $\overline{a}+\overline{b}$ | C. | $\frac{1}{n}(\overline{a}+\overline{b})$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线 y=-x2+mx+4m 的图象与x轴交于A、B两点,与y轴交于点C(0,8).
如图,已知抛物线 y=-x2+mx+4m 的图象与x轴交于A、B两点,与y轴交于点C(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
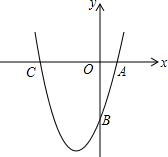 如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
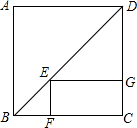 如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.
如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 墙上钉木条,至少用两颗钉子,运用的是“两点确定一条直线”的原理 | |
| B. | 射线OA与射线AO是同一条射线 | |
| C. | 延长线段AB到C,使AC=BC | |
| D. | 如果AC=BC,则点C是线段AB的中点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com