
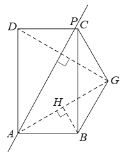
【题目】四边形![]() 是矩形,点
是矩形,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() .
.
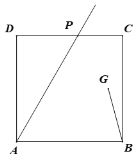
(1)如图,若四边形![]() 是正方形,求
是正方形,求![]() 的度数;
的度数;
(2)连接![]() ,设
,设![]() 探究当
探究当![]() 时a与b的数量关系.
时a与b的数量关系.
【答案】(1)15°;(2)a=![]() b或 a=
b或 a=![]() b
b
【解析】
(1)连接DG,交AP于点E,连接AG,根据对称的性质和正方形的性质,可以求到AG=AB,∠GAB=30°,再结合等腰三角形的性质即可求得答案;
(2)连接DG,AG,先判断△ADG是等边三角形,根据等边三角形的性质和矩形的性质推到△GAB≌△GDC;当∠CGB=120°时,点G可能在矩形ABCD的内部或外部,所以这里需要分两种情况,分别画图求解即可.
(1)解:连接DG,交AP于点E,连接AG,
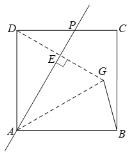
∵点G与点D关于直线AP对称,
∴AP垂直平分DG,
∴AD=AG.
∵在△ADG中,AD=AG,AE⊥DG,
∴∠PAG=∠PAD=30°.
又∵在正方形ABCD中,AD=AB,∠DAB=∠ABC=90°
∴AG=AB,∠GAB=∠DAB-∠PAD-∠PAG=30°,
∴在△GAB中,∠ABG=∠AGB=![]() =75°
=75°
∴∠GBC=∠ABC-∠ABG=15°
(2)解:连接DG,AG,
由(1)可知,在△ADG中,AD=AG,
∠DAG=∠PAD+∠PAG=60°,
∴△ADG是等边三角形,
∴DG=AG=AD,∠DAG=∠ADG=∠DGA=60°,
又∵ 在矩形ABCD中,AB=DC,∠DAB=∠ADC=∠ABC=90°,
∴∠DAB-∠DAG=∠ADC-∠ADG,
即∠GAB=∠GDC=30°,
∴△GAB≌△GDC,
∴GB=GC;
当∠CGB=120°时,点G可能在矩形ABCD的内部或外部,
若点G在矩形ABCD的内部,
∵在△BGC中,GB=GC,∠CGB=120°,
∴∠GBC=![]() =30°,
=30°,
∴∠GBA=∠ABC-∠GBC=90°-30°=60°,
在△ABG中,∠AGB=180°-∠GAB-∠GBA=90°,
∴在Rt△ABG中,cos∠GAB=![]() ,
,
∴a=![]() b,
b,
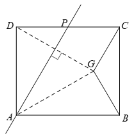
若点G在矩形ABCD的外部,
在△BGC中,∠GBC=30°,
∴∠ABG=120°,
又∵∠GAB=30°,
∴∠AGB=180°-30°-120°=30°,
∴BA=BG,
过点B作BH⊥AG,垂足为H,
∴AH=![]() AG=
AG=![]() b,
b,
在Rt△ABH中,∠AHB=90°,∠HAB=30°,
∴cos∠HAB=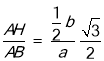 ,
,
∴a=![]() b,
b,
在Rt△ADP中,∠ADP=90°,∠PAD=30°,
∴tan∠PAD=![]() ,
,
∴DP=![]() b;
b;
所以无论点G在矩形ABCD内部还是点G在矩形ABCD外部,都有DP≤DC,均符合题意;
综上,当∠CGB=120°时a与b的数量关系为a=![]() b或 a=
b或 a=![]() b.
b.


科目:初中数学 来源: 题型:
【题目】(12分)如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
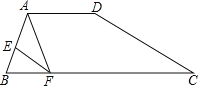
(1)求CF的长;
(2)若∠BFE=∠FAB,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
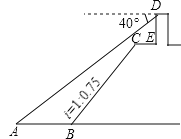
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交 线段CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交 线段CD于点E,设点P的横坐标为m.
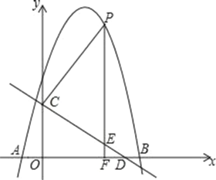
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以P、Q、C、D为顶点的四边形是平行四边形是否存在?若存在,请直接写出存在 个满足题意的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
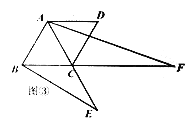
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE连接BE

(1)发现问题:如图①,若E是线段AC的中点,连接EF,其他条件不变,猜想线段BE与EF的数量关系
(2)探究问题:如图②,若E是线段AC上任意一点,连接EF,其他条件不变,猜想线段BE与EF的数量关系是什么?请证明你的猜想
(3)解决问题:如图③,若E是线段AC延长线上任意一点,其他条件不变,且∠EBC=30°,AB=3请直接写出AF的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=5,BC=12.如果分别以A、C为圆心的两圆外切,且圆A与直线BC相交,点D在圆A外,那么圆C的半径长r的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
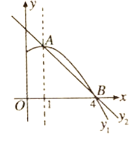
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点是
图象的一部分,抛物线的顶点是![]() ,对称轴是直线
,对称轴是直线![]() ,且抛物线与
,且抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;直线
;直线![]() 的解析式为
的解析式为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与
有两个不相等的实数根;④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;⑤当
;⑤当![]() 时,则
时,则![]() .其中正确的是( )
.其中正确的是( )
A.①②B.①③⑤C.①④D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
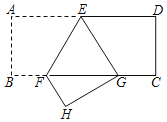
【题目】如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com