
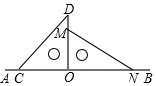
 如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周,在旋转的过程中,当第5.5或11.5秒时,直线CD恰好与直线MN垂直.
如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周,在旋转的过程中,当第5.5或11.5秒时,直线CD恰好与直线MN垂直. 分析 分CD在OM的右边时,设CD与AB相交于G,根据直角三角形两锐角互余求出∠CGN,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CON,再求出旋转角即可,CD在OM的左边时,设CD与AB相交于G,根据直角三角形两锐角互余求出∠NGD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠AOC,然后求出旋转角,计算即可得解.
解答 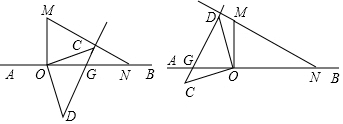 解:如图,CD在OM的右边时,设CD与AB相交于G,
解:如图,CD在OM的右边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGC=90°-∠MNO=90°-30°=60°,
∴∠CON=∠NGC-∠OCD=60°-45°=15°,
∴旋转角为180°-∠CON=180°-15°=165°,
t=165°÷30°=5.5秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°-∠MNO=90°-30°=60°,
∴∠AOC=∠NGD-∠C=60°-45°=15°,
∴旋转角为360°-∠AOC=360°-15°=345°,
t=345°÷30°=11.5秒,
综上所述,第5.5或11.5秒时,直线CD恰好与直线MN垂直.
故答案为:5.5或11.5.
点评 本题考查了旋转的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,熟记各性质并熟悉三角板的度数特点是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
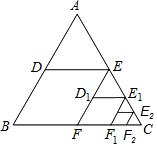 如图,△ABC三边AB、AC、BC的中点分别D、E、F,连接得四边形DEFB,它的面积记作为S1,取△EFC三边中点D1、E1、F1,连接得四边形D1E1F1F,它的面积记作S2,取△E1F1C三边的中点,D2、E2、F2,连接得四边形D2E2F2F1,它的面积记作S3,…,按规律依次作图,若△ABC的面积为1,则四边形D5E5F5F4的面积S6为( )
如图,△ABC三边AB、AC、BC的中点分别D、E、F,连接得四边形DEFB,它的面积记作为S1,取△EFC三边中点D1、E1、F1,连接得四边形D1E1F1F,它的面积记作S2,取△E1F1C三边的中点,D2、E2、F2,连接得四边形D2E2F2F1,它的面积记作S3,…,按规律依次作图,若△ABC的面积为1,则四边形D5E5F5F4的面积S6为( )| A. | $\frac{1}{{2}^{5}}$ | B. | $\frac{1}{{2}^{6}}$ | C. | $\frac{1}{{2}^{10}}$ | D. | $\frac{1}{{2}^{11}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 175 | 173 | 174 | 175 |
| 方差(cm2) | 3.5 | 3.5 | 12.5 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com