
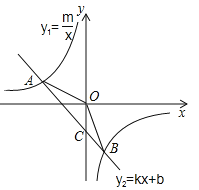
【题目】如图,已知反比例函数y1=![]() 的图像与一次函数y2=kx+b的图象交于两点A(-2,1)、B(a,-2).
的图像与一次函数y2=kx+b的图象交于两点A(-2,1)、B(a,-2).
(1)求反比例函数和一次函数的解析式;
(2)若一次函数y2=kx+b的图象交y轴于点C,求△AOB的面积(O为坐标原点);
(3)求使y1>y2时x的取值范围.
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() ;(3)-2<x<0或x>1.
;(3)-2<x<0或x>1.
【解析】试题分析:(1)先根据点A的坐标求出反比例函数的解析式为y1=-![]() ,再求出B的坐标是(1,-2),利用待定系数法求一次函数的解析式;
,再求出B的坐标是(1,-2),利用待定系数法求一次函数的解析式;
(2)在一次函数的解析式中,令x=0,得出对应的y2的值,即得出直线y2=-x-1与y轴交点C的坐标,从而求出△AOB的面积;
(3)当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围-2<x<0或x>1.
试题解析:(1)∵函数y1=![]() 的图象过点A(-2,1),即1=
的图象过点A(-2,1),即1=![]() ,
,
∴m=-2,即y1=![]() ,
,
∵点B(a,-2)在y1=![]() 上,∴a=1,∴B(1,-2),
上,∴a=1,∴B(1,-2),
又∵一次函数y2=kx+b过A、B两点,
即![]() ,解得:
,解得: ![]() ,
,
∴y2=-x-1;
(2)∵x=0,∴y2=-x-1=-1,
即y2=-x-1与y轴交点C(0,-1),
∴S△AOB=S△AOC+S△BOC=![]() =
=![]() ;
;
(3)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴-2<x<0,或x>1.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
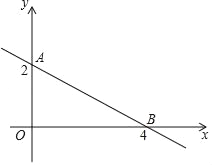
【题目】如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.
(1)求直线AB的表达式及△AOB的面积S△AOB.
(2)在x轴上是否存在一点,使S△PAB=3?若存在,求出P点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“滴滴”司机沈师傅从上午8:00~9:15在东西方向的江平大道上营运,共连续运载十批乘客.若规定向东为正,向西为负,沈师傅营运十批乘客里程如下:(单位:千米)+8,-6,+3,-6,+8,+4,-8,-4,+3,+3.
(1)将最后一批乘客送到目的地时,沈师傅距离第一批乘客出发地的东面还是西面?距离多少千米?
(2) 若汽车每千米耗油0.4升,则8:00~9:15汽车共耗油多少升?
(3)若“滴滴”的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米2元.则沈师傅在上午8:00~9:15一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车;而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆车的舒适程度比第一辆好,他就上第二辆车;如果第二辆不比第一辆好,他就上第三辆车.如果把这三辆车的舒适程度分为上、中、下三等,请解决下面的问题:
(1)三辆车按出现的先后顺序共有_____种不同的可能.
(2)你认为甲、乙两人所采用的方案中,不巧坐到下等车的可能性大小比较为:_____(填“甲大”、“乙大”、“相同”).理由是:_____.(要求通过计算概率比较)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C是线段AB的中点
(1)如图,若点D在线段CB上,且BD=1.5厘米,AD=6.5厘米,求线段CD的长度;
![]()
(2)若将(1)中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再解答.
我们在判断点(-7,20)是否在直线y=2x+6上时,常用的方法是:把x=-7代入y=2x+6中,由2×(-7)+6=-8≠20,判断出点(-7,20)不在直线y=2x+6上.小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆,你认为他的推断正确吗?请你利用上述方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com