
【题目】一位同学拿了两块45°的三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.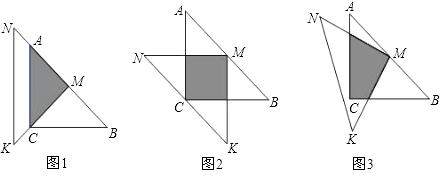
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 , 周长为;
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 , 周长为;
(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
【答案】
(1)![]() ;(1+
;(1+ ![]() )a
)a
(2)![]() a2
a2![]() ;2a
;2a
(3)
解:猜想:重叠部分的面积为 ![]() .
.
理由如下:
过点M分别作AC、BC的垂线MH、MG,垂足为H、G
设MN与AC的交点为E,MK与BC的交点为F
∵M是△ABC斜边AB的中点,AC=BC=a
∴MH=MG= ![]()
又∵∠HME+∠HMF=∠GMF+∠HMF,
∴∠HME=∠GMF,
∴Rt△MHE≌Rt△MGF
∴阴影部分的面积等于正方形CGMH的面积
∵正方形CGMH的面积是MGMH= ![]() ×
× ![]() =
= ![]()
∴阴影部分的面积是 ![]() .
.

【解析】解:(1)∵AM=MC= ![]() AC=
AC= ![]() a,则
a,则
∴重叠部分的面积是△ACB的面积的一半为 ![]() a2 , 周长为(1+
a2 , 周长为(1+ ![]() )a.(2)∵重叠部分是正方形
)a.(2)∵重叠部分是正方形
∴边长为 ![]() a,面积为
a,面积为 ![]() a2 , 周长为2a.
a2 , 周长为2a.
(1)由等腰直角三角形的性质:底边上的中线与底边上的高重合,得到△AMC是等腰直角三角形,AM=MC= ![]() AC=
AC= ![]() a,则重叠部分的面积是△ACB的面积的一半,为
a,则重叠部分的面积是△ACB的面积的一半,为 ![]() a2 , 周长为(1+
a2 , 周长为(1+ ![]() )a.(2)易得重叠部分是正方形,边长为
)a.(2)易得重叠部分是正方形,边长为 ![]() a,面积为
a,面积为 ![]() a2 , 周长为2a.(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.
a2 , 周长为2a.(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2 , 此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2 , 此时AP2= ![]() +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3= ![]() +2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
+2…按此规律继续旋转,直至得到点P2026为止,则AP2016= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24
(1)求CD的长;
(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. 
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 现有一动点P,从A点出发,沿着三角形的边AC-CB-BA运动,回到A点停止,速度为1 cm/s,设运动时间为t s.
(1)当t=_______时,△ABC的周长被线段AP平分为相等的两部分.
(2)当t=_______时,△APC的面积等于△ABC面积的一半.
(3)还有一个△DEF,∠E=90°,如图②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的边上,若另外有一个动点Q,与P 同时从A点出发,沿着边AB-BC-CA运动,回到点A停止. 在两点运动过程中某一时刻,恰好△APQ与△DEF全等,则点Q的运动速度 cm/s.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地. 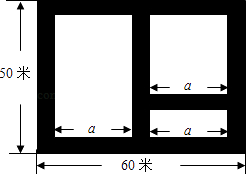
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数. 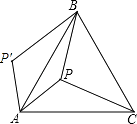
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,AD与BE相交于点F,且AE=CD.
(1)求证:AD=BE;
(2)求∠BFD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com