
 我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.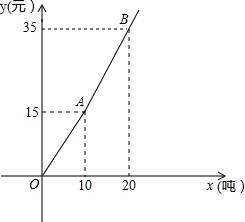 解:(1)如图,a=
解:(1)如图,a=| 15 |
| 10 |
| 35-15 |
| 20-10 |
|
|
|
|


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
 如图,在由相同的小正方形组成的网格中,正方形OABC的顶点都在格点上,将正方形OABC绕点O逆时针旋转一定的角度后,边OA的对应边OA′.
如图,在由相同的小正方形组成的网格中,正方形OABC的顶点都在格点上,将正方形OABC绕点O逆时针旋转一定的角度后,边OA的对应边OA′.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com