
【题目】(1)阅读理解:
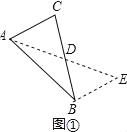
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
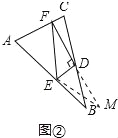
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
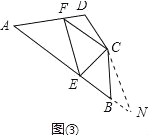
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

【答案】(1)2<AD<8;(2)证明详见解析;(3)BE+DF=EF;理由详见解析.
【解析】
试题分析:(1)延长AD至E,使DE=AD,由SAS证明△ACD≌△EBD,得出BE=AC=6,在△ABE中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;
(2)延长FD至点M,使DM=DF,连接BM、EM,同(1)得△BMD≌△CFD,得出BM=CF,由线段垂直平分线的性质得出EM=EF,在△BME中,由三角形的三边关系得出BE+BM>EM即可得出结论;
(3)延长AB至点N,使BN=DF,连接CN,证出∠NBC=∠D,由SAS证明△NBC≌△FDC,得出CN=CF,∠NCB=∠FCD,证出∠ECN=70°=∠ECF,再由SAS证明△NCE≌△FCE,得出EN=EF,即可得出结论.
试题解析:(1)解:延长AD至E,使DE=AD,连接BE,如图①所示:
∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,BD=CD,∠BDE=∠CDA,DE=AD,
∴△BDE≌△CDA(SAS),
∴BE=AC=6,
在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,
∴10﹣6<AE<10+6,即4<AE<16,
∴2<AD<8;
故答案为:2<AD<8;
(2)证明:延长FD至点M,使DM=DF,连接BM、EM,如图②所示:
同(1)得:△BMD≌△CFD(SAS),
∴BM=CF,
∵DE⊥DF,DM=DF,
∴EM=EF,
在△BME中,由三角形的三边关系得:BE+BM>EM,
∴BE+CF>EF;
(3)解:BE+DF=EF;理由如下:
延长AB至点N,使BN=DF,连接CN,如图3所示:
∵∠ABC+∠D=180°,∠NBC+∠ABC=180°,
∴∠NBC=∠D,
在△NBC和△FDC中,
BN=DF,∠NBC =∠D,BC=DC,
∴△NBC≌△FDC(SAS),
∴CN=CF,∠NCB=∠FCD,
∵∠BCD=140°,∠ECF=70°,
∴∠BCE+∠FCD=70°,
∴∠ECN=70°=∠ECF,
在△NCE和△FCE中,
CN=CF,∠ECN=∠ECF,CE=CE,
∴△NCE≌△FCE(SAS),
∴EN=EF,
∵BE+BN=EN,
∴BE+DF=EF.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( ).
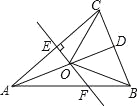
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至5月21日,全县完成工业开票销售337.53亿元,337.53亿元用科学计数法表示为( )元.
A. 33.753×109 B. 3.3753×1010 C. 0.33753×1011 D. 0.033753×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 全等三角形是指形状相同的三角形
B. 全等三角形是指面积相等的三角形
C. 全等三角形的周长和面积都相等
D. 所有的等边三角形都全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.

(1)求证:DE=AB.
(2)以D为圆心, DE为半径作圆弧交AD于点G.若BF=FC=1,试求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com